题目内容
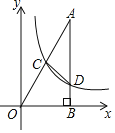
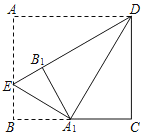
【题目】如图，在矩形ABCD中，AD＝4，将∠A向内翻析，点A落在BC上，记为A1，折痕为DE．若将∠B沿EA1向内翻折，点B恰好落在DE上，记为B1，则AB＝_____．
【答案】
【解析】
依据△A1DB1≌△A1DC（AAS），即可得出A1C＝A1B1，再根据折叠的性质，即可得到A1C＝
BC＝2，最后依据勾股定理进行计算，即可得到CD的长，即AB的长．
解：由折叠可得，A1D＝AD＝4，∠A＝∠EA1D＝90°，∠BA1E＝∠B1A1E，BA1＝B1A1，∠B＝∠A1B1E＝90°，
∴∠EA1B1+∠DA1B1＝90°＝∠BA1E+∠CA1D，
∴∠DA1B1＝∠CA1D，
又∵∠C＝∠A1B1D，A1D＝A1D，
∴△A1DB1≌△A1DC（AAS），
∴A1C＝A1B1，
∴BA1＝A1C＝BC＝2，
∴Rt△A1CD中，CD＝
＝，
∴AB＝.
故答案为：．
练习册系列答案
相关题目
【题目】小王计划批发“山东大樱桃”和“泰国榴莲”两个品种的水果共120斤，樱桃和榴莲的批发价分别为32元/斤和40元/斤.设购买了樱桃x斤
.
（1）若小王批发这两种水果正好花费了4400元，那么小王分别购买了多少斤樱桃和榴莲？填写下表，并列方程求解；
品种 | 批发价（元） | 购买斤数 | 小王应付的钱数（元） |
樱桃 | 32 | x | |
榴莲 | 40 |
（2）设小王购买两种水果的总花费为y元，试写出y与x之间的函数表达式.
（3）若要求所批发的榴莲的斤数不少于樱桃斤数的2倍，那么购买樱桃的数量为多少时，可使小王的总花费最少？这个最少花费是多少？
