题目内容
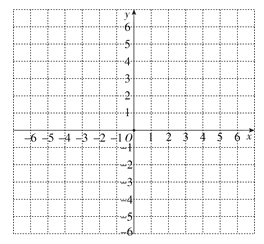
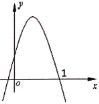
【题目】二次函数![]() 的图象如图所示,则下列结论:
的图象如图所示,则下列结论:
① ![]() ②
②![]() ③
③![]() ④
④![]() ⑤
⑤![]() 其中正确的个数是( )
其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:①由图象可知:抛物线开口方向向下,则a<0,对称轴直线位于y轴右侧,根据“左同右异”,则a、b异号,即b>0,抛物线与y轴交于正半轴,则c>0,abc<0,故①错误;
②∵对称轴为x=![]() <1,又a<0,则2a+b<0,故②错误;
<1,又a<0,则2a+b<0,故②错误;
③当x=-1时,y<0,∴a-b+c<0,故③正确;
④抛物线与x轴有两个不同的交点,则b2-4ac>0,所以4ac-b2<0,故④正确;
⑤当x=1时,y=0,∴a+b+c=0,又c>0,则a+b<0,故⑤正确;
综上所述,正确结论有3个;
故选:C.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目