题目内容
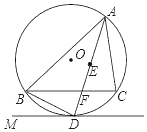
【题目】如图,⊙O是△ABC的外接圆,点E为△ABC内切圆的圆心,连接AE的延长线交BC于点F,交⊙O于点D;连接BD,过点D作直线DM,使∠BDM=∠DAC.
(1)求证:直线DM是⊙O的切线;
(2)若DF=2,且AF=4,求BD和DE的长.
【答案】(1)证明见解析(2)2![]()
【解析】
(1)根据垂径定理的推论即可得到OD⊥BC,再根据∠BDM=∠DBC,即可判定BC∥DM,进而得到OD⊥DM,据此可得直线DM是⊙O的切线;
(2)根据三角形内心的定义以及圆周角定理,得到∠BED=∠EBD,即可得出DB=DE,再判定△DBF∽△DAB,即可得到DB2=DFDA,据此解答即可.
(1)如图所示,连接OD.
∵点E是△ABC的内心,∴∠BAD=∠CAD,∴![]() ,∴OD⊥BC.
,∴OD⊥BC.
又∵∠BDM=∠DAC,∠DAC=∠DBC,∴∠BDM=∠DBC,∴BC∥DM,∴OD⊥DM.
又∵OD为⊙O半径,∴直线DM是⊙O的切线.
(2)连接BE.∵E为内心,∴∠ABE=∠CBE.
∵∠BAD=∠CAD,∠DBC=∠CAD,∴∠BAD=∠DBC,∴∠BAE+∠ABE=∠CBE+∠DBC,即∠BED=∠DBE,∴BD=DE.
又∵∠BDF=∠ADB(公共角),∴△DBF∽△DAB,∴![]() ,即DB2=DFDA.
,即DB2=DFDA.
∵DF=2,AF=4,∴DA=DF+AF=6,∴DB2=DFDA=12,∴DB=DE=2![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】甲乙两个仓库要向A、B两地运送水泥,已知甲库可调出100吨水泥,乙库可调出80吨水泥,A地需70吨水泥,B地需110吨水泥,两库到A,B两地的路程和运费如下表(表中运费栏“元/(吨、千米)”表示每吨水泥运送1千米所需人民币)(本题满分10分)
路程/千米 | 运费(元/吨、千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A地 | 20 | 15 | 12 | 12 |
B地 | 25 | 20 | 10 | 8 |
(1)设甲库运往A地水泥![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式;
(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两地多少吨水泥时,总运费最省?最省的总运费是多少?