Question

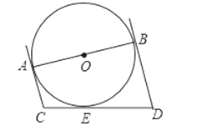
【题目】如图，⊙O的直径AB=18，AC和BD是它的两条切线，CD与⊙O相切于E，且与AC、BD相交于点C、D，设AC=x，BD=y，试求xy的值．

Answer 1

【答案】81

【解析】

连接OC，OD，根据勾股定理可得出OC和OD，再由切线的性质得出△OCD是直角三角形，根据勾股定理得出xy的值

连接OC，OD．

∵AB=18，∴OA=OB=9，

∵AC和BD是它的两条切线，

∴OA⊥AC，OB⊥BD，

∴AC∥BD，

∴∠ACD+∠BDE=180°，

∴∠OCD+∠ODC=90°，

∵AC=x，BD=y，

∴OC=，OD=，

∵CD是圆O的切线，

∴CE=AC=x，DE=BD=y，

∴OC2+OD2=CD2 ，

即x2+81+y2+81=（x+y）2 ，

整理得2xy=162，

∴xy=81．