题目内容
【题目】已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN.
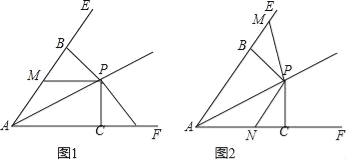
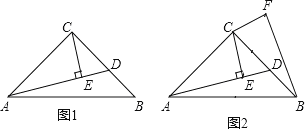
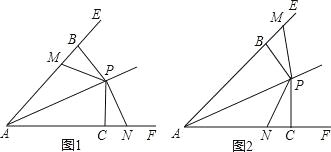
(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;
(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系 ;
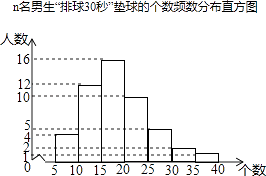
(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.
【答案】(1)、证明过程见解析;(2)、AM+AN=2AC;(3)、32
【解析】
试题分析:(1)、根据PB=PC,∠PBM=∠PCN=90°,利用HL判定Rt△PBM≌Rt△PCN,即可得出BM=CN;
(2)、先已知条件得出AP平分∠CPB,再根据PB⊥AB,PC⊥AC,得到AB=AC,最后根据BM=CN,得出AM+AN=(AB﹣MB)+(CN+AC)=AB+AC=2AC;(3)、由AC:PC=2:1,PC=4,即可求得AC的长,又由S四边形ANPM=S△APN+S△APB+S△PBM=S△APN+S△APB+S△PCN=S△APC+S△APB,即可求得四边形ANPM的面积.
试题解析:(1)、如图1,∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°, ∵在Rt△PBM和Rt△PCN中,PBM=∠PCN=90°,
![]() , ∴Rt△PBM≌Rt△PCN(HL), ∴BM=CN;
, ∴Rt△PBM≌Rt△PCN(HL), ∴BM=CN;
(2)、AM+AN=2AC. ∵∠APB=90°﹣∠PAB,∠APC=90°﹣∠PAC,点P为∠EAF平分线上一点,
∴∠APC=∠APB,即AP平分∠CPB, ∵PB⊥AB,PC⊥AC, ∴AB=AC, 又∵BM=CN,
∴AM+AN=(AB﹣MB)+(CN+AC)=AB+AC=2AC;
(3)、如图2,∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF, ∴PB=PC,∠PBM=∠PCN=90°,
∵在Rt△PBM和Rt△PCN中,PBM=∠PCN=90°, ![]() , ∴Rt△PBM≌Rt△PCN(HL),
, ∴Rt△PBM≌Rt△PCN(HL),
∴BM=CN, ∴S△PBM=S△PCN ∵AC:PC=2:1,PC=4, ∴AC=8,
∴由(2)可得,AB=AC=8,PB=PC=4, ∴S四边形ANPM=S△APN+S△APB+S△PBM =S△APN+S△APB+S△PCN
=S△APC+S△APB =![]() ACPC+
ACPC+![]() ABPB=
ABPB=![]() ×8×4+
×8×4+![]() ×8×4=32.
×8×4=32.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案