��Ŀ����
����Ŀ��(1)��֪����P(a��b)��P����������![]() +|3a��2b��4|��0��45���ǵ����ǰ壬ֱ�Ƕ������P���������������ύ��A��B���㣬��ͼ1����a��b��ֵ.
+|3a��2b��4|��0��45���ǵ����ǰ壬ֱ�Ƕ������P���������������ύ��A��B���㣬��ͼ1����a��b��ֵ.
(2)�����ǰ���P�㣬˳ʱ����ת��������x�ύ��B�㣬��y�ύ��A�㣬��|OA��OB|��ֵ.
(3)��ͼ3����Q���߶�AB��һ���㣬CΪAQ�е㣬PR��PQ��PR��PQ����BR����ͬѧ���ж��߶�BR��PC֮��Ĺ�ϵ��������֤��.
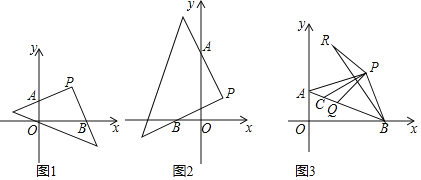
���𰸡�(1)a=4��b=4��(2)|AO��OB��8��(3)BR��2PC��PC��BR�����ɼ�����.
��������
(1)���÷Ǹ��������ʽ�����⼴��.
(2)��ͼ2�У���PE��OB��E��PF��OA��F.֤����AFP�ա�BEP(ASA)���Ƴ�AF��BE���ɽ������.
(3)���ۣ�BR��2PC��PC��BR.��ͼ3�У��ӳ�PC��G��ʹ��CG��PC������AG��GQ����PG��BR��J.֤����GAP�ա�RPB(SAS)���ɽ������.
(1)��![]() +|3a��2b��4|��0��
+|3a��2b��4|��0��
��![]() ��
��
��ã�![]() ��
��
(2)��ͼ2�У���PE��OB��E��PF��OA��F.

��P(4��4)��
��PE��PF��4���ı���OEPF�������Σ�
���EPF����QPB��90����OF��OE��PE��PF��4��
���APF����BPE��
�ڡ�AFP�͡�BEP�У�
 ��
��
���AFP�ա�BEP(ASA)��
��AF��BE��
��|AO��OB��|OF+AF��(BE��OE)|��OF+OE��8.
(3)���ۣ�BR��2PC��PC��BR.�������£�
��ͼ3�У��ӳ�PC��G��ʹ��CG��PC������AG��GQ����PG��BR��J.

��AC��CQ��PC��CG��
���ı���AGQP��ƽ���ı��Σ�
��AG��PQ��PR��AG��PQ��
���GAP+��APQ��180����
�ߡ�APB����RPQ��90����
���APR+��APQ+��APQ+��BPQ��180����
���RPB+��APQ��180����
���GAP����BPQ��
�ڡ�GAP�͡�RPB�У�
 ��
��
���GAP�ա�RPB(SAS)��
��PG��BR����APG����PBR��
�ߡ�APG+��JPB��90����
���JPB+��PBR��90����
���PJB��90����
��PC��BR��BR��2PC.

����Ŀ�����⣺̽��������ͼ�������ʣ�С������ѧϰ�����ľ��飬�Ժ�����ͼ�������ʽ�����̽����������С����̽�����̣��벹���������ں���y��|x|��2�У��Ա���x����������ʵ����
�������y��x�ļ����Ӧֵ��
y | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | �� |
x | �� | 1 | 0 | ��1 | ��2 | ��1 | 0 | m | �� |
��m���� ����
����A��n��8����B��10��8��Ϊ�ú���ͼ���ϲ�ͬ�����㣬��n���� ����
����ͼ����ƽ��ֱ������ϵxOy�У�������ϱ��и��Զ�ӦֵΪ����ĵ㣮����������ĵ㣬�����ú�����ͼ���ݺ���ͼ��ɵã�
���ú�������СֵΪ�� ����
���ú�������һ���������� ����