Question

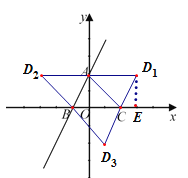
【题目】如图，在平面直角坐标系中，点A、B、C的坐标分别为（0,2）、（-1,0）、（2,0）.

（1）求直线AB的函数表达式；

（2）直线AB上有一点P，使得△PBC的面积等于9，求点P的坐标；

（3）设点D与A、B、C 点构成平行四边形，直接写出所有符合条件的点D的坐标.

Answer 1

【答案】（1）y=2x+2；（2）（2，6）或（-4，-6）；（3）（3，2）、（-3，2）、（1，-2）

【解析】

（1）根据待定系数法，可得函数解析式；

（2）设点P的坐标为（x，2x+2），根据三角形的面积公式列方程求解即可；

（3）分三种情况求解即可：①当AB、BC为邻边时，②当AB为对角线时，③当BC为对角线时．

解：（1）设直线AB的函数解析式为y=kx+b，

∵直线AB经过点A（0，2）、B（-1，0），得

，

解得．

∴直线AB的函数解析式为y=2x+2；

（2）由题意，设点P的坐标为（x，2x+2），

S△POA=×BC×|py|=×3×|2x+2|=9．

解得x=2或x=-4．

故点P的坐标是（2，6）或（-4，-6）；

（3）①当AB、BC为邻边时，作D1E⊥BC于E，

∵四边形ABCD1是平行四边形，

∴AD1=BC=3，AB=CD1，∠ABC=∠D1CE，

又∵∠AOB=∠D1EC，

∴△AOB≌△D1EC，

∴CE=BO=1，

∴D1（3，2）；

同理可求：

②当AB为对角线时，D2（-3，2）；

③当BC为对角线时，D3（1，-2）；

综上所述：点D与A、B、C点构成平行四边形，点D的坐标为（3，2）、（-3，2）、（1，-2）．