题目内容
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交于BE的延长线于点F.
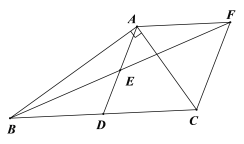
(1)求证:△AEF≌△DEB;
(2)若AC=4,AB=5,求菱形ADCF的面积.
【答案】(1)详见解析;(2)10.
【解析】
(1)根据AAS证△AFE≌△DBE;
(3)由直角三角形ABC与菱形有相同的高,根据等积变形求出这个高,代入菱形面积公式可求出结论.
(1)证明:①∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
∠AFE=∠DBE,∠FEA=∠BED,AE=DE
∴△AFE≌△DBE(AAS);
(2)由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=1212BC,
∴四边形ADCF是菱形;
连接DF,
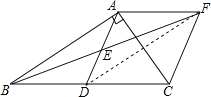
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S菱形ADCF=![]() =
=![]() ×4×5=10.
×4×5=10.

【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

【题目】甲、乙两名同学的家与学校的距离均为![]() .甲同学先步行
.甲同学先步行![]() ,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的
,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的![]() 倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到
倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到![]() .
.
(1)解:设乙同学骑自行车的速度为![]() .完成表格:
.完成表格:
乙同学 | 甲同学 | ||
骑自行车 | 步行 | 乘公交车 | |
路程 |
|
| |
时间 |
| ||
(2)求乙同学骑自行车的速度.
(3)当甲同学到达学校时,乙同学离学校还有多少米?