题目内容
【题目】问题:探究函数的图象与性质.小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:在函数y=|x|﹣2中,自变量x可以是任意实数;
Ⅰ如表是y与x的几组对应值.
y | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
x | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m= ;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n= ;
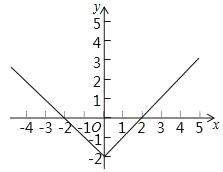
Ⅱ如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;根据函数图象可得:
①该函数的最小值为 ;
②该函数的另一条性质是 .
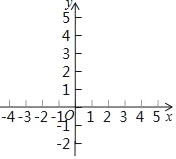
【答案】Ⅰ①1②-10;Ⅱ①-2②当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小
【解析】
Ⅰ①把x=3代入y=|x|﹣2,即可求出m;
②把y=8代入y=|x|﹣2,即可求出n;
Ⅱ①画出该函数的图象即可求解;
②根据图象可得增减性.
解:Ⅰ①把x=3代入y=|x|﹣2,得m=3﹣2=1.
故答案为1;
②把y=8代入y=|x|﹣2,得8=|x|﹣2,
解得x=﹣10或10,
∵A(n,8),B(10,8)为该函数图象上不同的两点,
∴n=﹣10.
故答案为﹣10;
Ⅱ该函数的图象如图所示,
①该函数的最小值为﹣2;
故答案为﹣2;
②当x>0时,y随x的增大而增大,
当x<0时,y随x的增大而减小.
故答案为:当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小.

 阅读快车系列答案
阅读快车系列答案【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减(辆) | -1 | +3 | -2 | -4 | +7 | -5 | -10 |
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?