题目内容
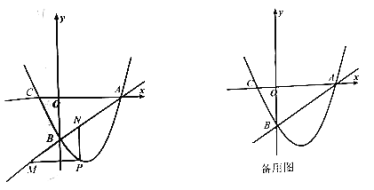
【题目】如图,已知平面直角坐标系![]() ,抛物线
,抛物线![]() 与
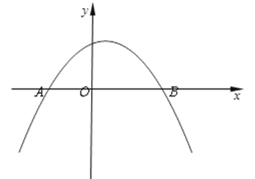
与![]() 轴交于点A(-2,0)和点B(4,0) .
轴交于点A(-2,0)和点B(4,0) .
(1)求这条抛物线的表达式和对称轴;
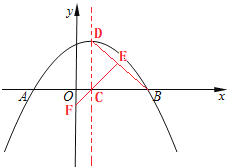
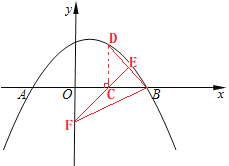
(2)点C在线段OB上,过点C作CD⊥![]() 轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与
轴,垂足为点C,交抛物线与点D,E是BD中点,联结CE并延长,与![]() 轴交于点F.
轴交于点F.
①当D恰好是抛物线的顶点时,求点F的坐标;
②联结BF,当△DBC的面积是△BCF面积的![]() 时,求点C的坐标.
时,求点C的坐标.
【答案】(1) ![]() ,x=1;(2)①F的坐标是(0,
,x=1;(2)①F的坐标是(0,![]() );②C坐标是
);②C坐标是![]() .
.
【解析】
(1)用待定系数法求解;
(2)①求出顶点坐标,得出DC、OC、BC长度,在Rt△DCB和Rt△OFC中,利用三角函数求出OF值即可;
②通过面积比找到DC与OF比值,证明△DCB∽△FOC,借助比例式求解OB,从而得到OC长.
(1)由题意得,抛物线![]() 经过点A(-2,0)和点B(4,0),
经过点A(-2,0)和点B(4,0),
代入得![]() 解得
解得 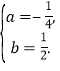
因此,这条抛物线的表达式是![]() .
.
它的对称轴是直线![]() .
.
(2)①由抛物线的表达式![]() ,得顶点D的坐标是(1,
,得顶点D的坐标是(1,![]() ).
).
∴![]() .
.
∵D是抛物线顶点,CD⊥![]() 轴,E是BD中点,∴
轴,E是BD中点,∴![]() . ∴
. ∴![]() .
.
∵![]() ,∴
,∴![]() .
.
在Rt△![]() 中,
中,![]() ,
,![]() .
.
在Rt△![]() 中,
中,![]() ,
,![]() .
.
∴![]() ,
,![]() .∴点F的坐标是(0,
.∴点F的坐标是(0,![]() ).
).
②∵![]() ,
,![]() , ∴
, ∴![]() .
.
∵△DBC的面积是△BCF面积的![]() , ∴
, ∴![]() .
.
由①得![]() ,又
,又![]() ,
,
∴△![]() ∽△
∽△![]() .∴
.∴![]() .
.
又OB=4,∴![]() ,∴
,∴![]() .即点C坐标是
.即点C坐标是![]() .
.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目