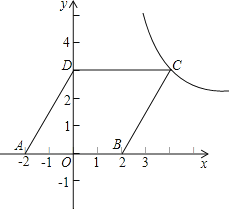题目内容
【题目】如图,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 点,抛物线
点,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于另一点
轴交于另一点![]() .
.
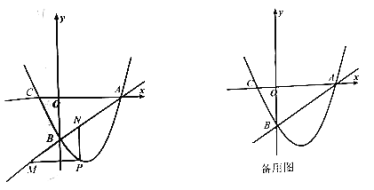
(1)求直线及抛物线的解析式;
(2)点![]() 是抛物线上一动点,当点
是抛物线上一动点,当点![]() 在直线
在直线![]() 下方的抛物线上运动时,过点
下方的抛物线上运动时,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)在(2)的条件下,当![]() 的值最大时,将
的值最大时,将![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 落在
落在![]() 轴上时,直接写出此时点
轴上时,直接写出此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时,![]() 有最大值,最大值为6;(3)点
有最大值,最大值为6;(3)点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)把点![]() 代入直线
代入直线![]() ,求出
,求出![]() 的值,即可求出直线的解析式,根据直线解析式求出点B的坐标,利用待定系数法即可求出抛物线的解析式;
的值,即可求出直线的解析式,根据直线解析式求出点B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)设![]() 点坐标为
点坐标为![]() ,则
,则![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,表示出
,表示出![]() ,
,![]() ,计算
,计算![]() 根据二次函数的性质进行求解即可.
根据二次函数的性质进行求解即可.
(3)当![]() 最大时
最大时![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ,分两种情况进行讨论即可.
,分两种情况进行讨论即可.
(1)把点![]() 代入直线
代入直线![]() 得:
得:![]() ,
,
∴![]() ,
,
∴![]() .
.
把点![]() ,
,![]() ,
,![]() 代入
代入![]() 得:
得:
 ,∴
,∴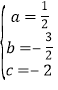 ,
,
∴![]() .
.
(2)设![]() 点坐标为
点坐标为![]() ,∵
,∵![]() 轴,
轴,![]() 轴,
轴,![]() 、
、![]() 在直线
在直线![]() 上,
上,
∴![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]()
![]() ,
,
∴当![]() 时,
时,![]() 有最大值,最大值为6.
有最大值,最大值为6.
(3)当![]() 最大时
最大时![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ,
,
∵![]() 为直角三角形,且
为直角三角形,且![]() ,
,![]() ,
,![]() ,
,
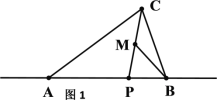
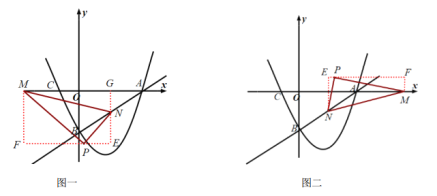
如图一:过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,交
,交![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,可得:
,可得:![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() 点坐标为
点坐标为![]() .
.
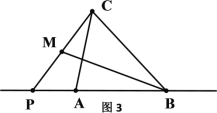
如图二:同理可得:![]() ,
,
∴![]() ,
,
设![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() ,
,
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
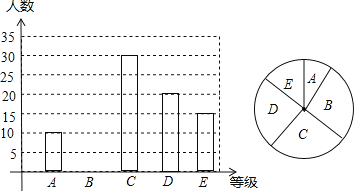
暑假作业北京艺术与科学电子出版社系列答案【题目】2019年,我省中考体育分值增加到55分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
成绩 | 3′40″及以下 | 3′41~4′ | 4′01″~4′20′ | 4′21″~4′40″ | 4′41″及以上 |
等级 | A | B | C | D | E |
百分比 | 10% | 25% | m | 20% | n |
(1)求样本容量及表格中的m和n的值
(2)求扇形统计图中A等级所对的圆心角度数,并补全统计图.
(3)我校9年级共有女生500人.若女生八百米成绩的达标成绩为4分,我校九年级女生八百米成绩达标的人数有多少?