Question

【题目】如图．在等边△ABC中，AC=8，点D，E，F分别在三边AB，BC，AC上，且AF=2，FD⊥DE，∠DFE=60°，则AD的长为 ．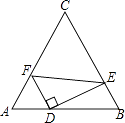

Answer 1

【答案】3
【解析】解：

∵∠DFE=60°，

∴∠1+∠2+60°=180°，

∴∠2=120°﹣∠1，

在等边△ABC中，∠A=∠C=60°，

∴∠A+∠1+∠3=180°，

∴∠3=180°﹣∠A﹣∠1=120°﹣∠1，

∴∠2=∠3，

又∵∠A=∠C，

∴△ADF∽△CFE，

∴ = ，

∵FD⊥DE，∠DFE=60°，

∴∠DEF=90°﹣60°=30°，

∴DF= EF，

又∵AF=2，AC=8，

∴CF=8﹣2=6，

∴ = ，

解得AD=3．

所以答案是：3．

【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识，掌握等边三角形的三个角都相等并且每个角都是60°，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．