题目内容
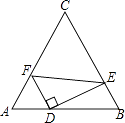
【题目】如图,在四边形ABCD中,∠A=90°,AD∥BC,E为AB的中点,连接CE,BD,过点E作FE⊥CE于点E,交AD于点F,连接CF,已知2AD=AB=BC.
(1)求证:CE=BD;
(2)若AB=4,求AF的长度;
(3)求sin∠EFC的值.
【答案】
(1)解:∵E为AB的中点,
∴AB=2BE,
∵AB=2AD,
∴BE=AD,
∵∠A=90°,AD∥BC,
∴∠ABC=90°,
在△ABD与△BCE中,  ,
,
∴△ABD≌△BCE,
∴CE=BD;
(2)解:∵AB=4,
∴AE=BE=2,BC=4,
∵FE⊥CE,
∴∠FEC=90°,
∴∠AEF+∠AFE=∠AEF+∠BEC=90°,
∴∠AFE=∠BEC,
∴△AEF∽△BCE,
∴ ![]() ,
,
∴AF=1;
(3)解:∵△AEF∽△BCE,
∴ ![]() ,
,
∴AF= ![]() AE,
AE,
设AF=k,则AE=BE=2k,BC=4k,
∴EF= ![]() =
= ![]() k,
k,
CE= ![]() =2
=2 ![]() k,
k,
∴CF= ![]() =5k,
=5k,
∴sin∠EFC= ![]() =
= ![]()
【解析】(1)由E为AB的中点,得到AB=2BE,等量代换得到BE=AD,推出△ABD≌△BCE,根据全等三角形的性质即可得到CE=BD;
(2)根据已知条件得到AE=BE=2,BC=4,根据余角的性质得到∠AFE=∠BEC,根据相似三角形的性质即可得到AF的长度;
(3)根据相似三角形的性质得到AF=![]() AE,设AF=k,则AE=BE=2k,BC=4k,根据勾股定理得到EF、CE、CF的值,再由三角函数的定义即可得到sin∠EFC的值.
AE,设AF=k,则AE=BE=2k,BC=4k,根据勾股定理得到EF、CE、CF的值,再由三角函数的定义即可得到sin∠EFC的值.
【考点精析】利用平行线的性质和勾股定理的概念对题目进行判断即可得到答案,需要熟知两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 阅读快车系列答案
阅读快车系列答案