题目内容
【题目】在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
①如图①,请直接写出AE与DF的数量关系______________;
②将△EBF绕点B逆时针旋转到图②所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;
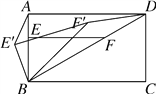
(2)如图③,若四边形ABCD为矩形,BC=mAB,其他条件都不变,将△EBF绕点B逆时针旋转α(0°<α<90°)得到△E′BF′,连接AE′,DF′,请在图③中画出草图,并求出AE′与DF′的数量关系.

【答案】(1)①DF=![]() AE
AE
②DF=![]() AE.理由见解析; (2) DF′=
AE.理由见解析; (2) DF′=![]() AE′.
AE′.
【解析】试题分析:
(1)①由四边形ABCD是正方形易得BD=![]() AB,由EF∥AD可得
AB,由EF∥AD可得![]() ,从而可DF=
,从而可DF=![]() AE;
AE;
②由旋转的性质结合题意可证△ABE∽△DBF可得![]() ,从而可得DF=
,从而可得DF=![]() AE;
AE;
(2)画图如下,由四边形ABCD为矩形,可得AD=BC=mAB,由勾股定理可得BD=![]() =
=![]() AB;易证△BEF∽△BAD,可得
AB;易证△BEF∽△BAD,可得![]() ,因此
,因此![]() =
=![]() .
.
由旋转性质结合题意可证△ABE′∽△DBF′,由此可得![]() =
=![]() =
=![]() ,
,
∴DF′=![]() AE′.
AE′.
试题解析:
(1)①DF=![]() AE
AE
②DF=![]() AE.理由如下:
AE.理由如下:
∵△EBF绕点B逆时针旋转到图②所示的位置,
∴∠ABE=∠DBF.
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴△ABE∽△DBF,
∴![]() ,即DF=
,即DF=![]() AE.
AE.
(2)如图所示,∵四边形ABCD为矩形,
∴AD=BC=mAB,
∴BD=![]() =
=![]() AB.
AB.
∵EF⊥AB,
∴EF∥AD,
∴△BEF∽△BAD,
∴![]() ,
,
∴![]() =
=![]() .
.
∵△EBF绕点B逆时针旋转α(0°<α<90°)得到△E′BF′,
∴∠ABE′=∠DBF′,BE′=BE,BF′=BF,
∴![]() =
=![]() =
=![]() ,
,
∴△ABE′∽△DBF′,
∴![]() =
=![]() =
=![]() ,即DF′=
,即DF′=![]() AE′.
AE′.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目

