题目内容
【题目】(1)求证:到线段两端距离相等的点在线段的垂直平分线上.(要求:画出图形,写出已知,求证和证明过程)
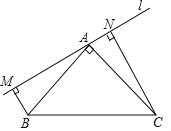
(2)用(1)中的结论解决:如图,△ABC中,∠A=30°,∠C=90°,BE平分∠ABC, 求证:点E在线段AB的垂直平分线上.
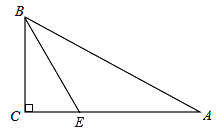
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)先画出图形,写出已知、求证,过Q作MN⊥AB于C,推出∠QCA=∠QCB=90°,根据HL推出Rt△QCA≌Rt△QCB,根据全等三角形的性质得出AC=BC,即可得出答案;(2)根据题意可得∠CBA=60°,由角平分线可得∠ABE=30°,即可证明∠ABE=∠A,可得BE=AE,根据(1)即可证明结论.
(1)已知:如图,QA=QB.
求证:点Q在线段AB的垂直平分线上.

证明:过点Q作MN⊥AB,垂足为点C.则∠QCA=∠QCB=90°
在Rt△QCA和Rt△QCB中,
∵QA=QB ,QC=QC
∴Rt△QCA≌Rt△QCB(H.L.)
∴AC=BC
∴点Q在线段AB的垂直平分线上.
即到线段两端距离相等的点在线段的垂直平分线上.
(2)证明:∵∠C=90°∠A=30°,
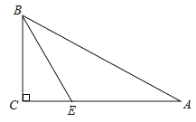
∴∠ABC=90°30°=60°,
∵BE平分∠ABC,
∴∠ABE=![]() ∠ABC=
∠ABC=![]() ×60°=30°,
×60°=30°,
∴∠A=∠ABE,
∴EA=EB,
∴点E在线段AB的垂直平分线上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目