题目内容
【题目】如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.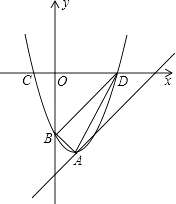
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
【答案】
(1)解:∵顶点A的横坐标为x=﹣ ![]() =1,且顶点A在y=x﹣5上,
=1,且顶点A在y=x﹣5上,
∴当x=1时,y=1﹣5=﹣4,
∴A(1,﹣4).
(2)解:△ABD是直角三角形.
将A(1,﹣4)代入y=x2﹣2x+c,可得,1﹣2+c=﹣4,∴c=﹣3,
∴y=x2﹣2x﹣3,∴B(0,﹣3)
当y=0时,x2﹣2x﹣3=0,x1=﹣1,x2=3
∴C(﹣1,0),D(3,0),
BD2=OB2+OD2=18,AB2=(4﹣3)2+12=2,AD2=(3﹣1)2+42=20,
BD2+AB2=AD2,
∴∠ABD=90°,即△ABD是直角三角形.
(3)解:存在.
由题意知:直线y=x﹣5交y轴于点E(0,﹣5),交x轴于点F(5,0)
∴OE=OF=5,
又∵OB=OD=3
∴△OEF与△OBD都是等腰直角三角形
∴BD∥l,即PA∥BD
则构成平行四边形只能是PADB或PABD,如图, 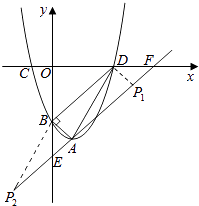
过点P作y轴的垂线,过点A作x轴的垂线交过P且平行于x轴的直线于点G.
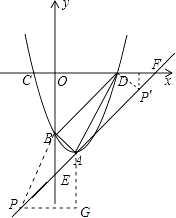
设P(x1,x1﹣5),则G(1,x1﹣5)
则PG=|1﹣x1|,AG=|5﹣x1﹣4|=|1﹣x1|
PA=BD=3 ![]()
由勾股定理得:
(1﹣x1)2+(1﹣x1)2=18,x12﹣2x1﹣8=0,x1=﹣2或4
∴P(﹣2,﹣7)或P(4,﹣1),
存在点P(﹣2,﹣7)或P(4,﹣1)使以点A、B、D、P为顶点的四边形是平行四边形.
【解析】(2)方法二:把A(1,﹣4)代入y=x2﹣2x+c,得c=﹣3,
∴y=x2﹣2x+3=(x﹣3)(x+1),
∴D(3,0),B(0,﹣3),A(1,﹣4),
KBD= ![]() =1,KAB=
=1,KAB= ![]() =﹣1,
=﹣1,
∴KBDKAB=﹣1,
∴AB⊥BD,即△ABD为直角三角形.
【考点精析】利用平行线的判定和等腰三角形的性质对题目进行判断即可得到答案,需要熟知同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;等腰三角形的两个底角相等(简称:等边对等角).