题目内容
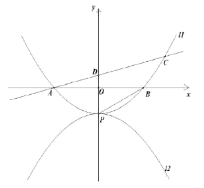
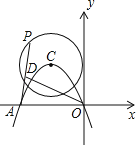
【题目】如图,已知在平面直角坐标系xOy中,O为坐标原点,抛物线y=﹣![]() x2+bx+c经过原点,与x轴的另一个交点为A(﹣6,0),点C是抛物线的顶点,且⊙C与y轴相切,点P为⊙C上一动点.若点D为PA的中点,连结OD,则OD的最大值是( )
x2+bx+c经过原点,与x轴的另一个交点为A(﹣6,0),点C是抛物线的顶点,且⊙C与y轴相切,点P为⊙C上一动点.若点D为PA的中点,连结OD,则OD的最大值是( )
A.![]() B.
B.![]() C.2
C.2![]() D.
D.![]()
【答案】B
【解析】
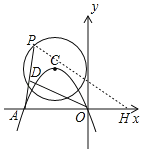
取点H(6,0),连接PH,由待定系数法可求抛物线解析式,可得点C坐标, 可得⊙C半径为4,由三角形中位线的定理可求OD=![]() PH, 当点C在PH上时,PH有最大值,即可求解.
PH, 当点C在PH上时,PH有最大值,即可求解.
如图,取点H(6,0),连接PH,
∵抛物线y=﹣![]() x2+bx+c经过原点,与x轴的另一个交点为A(﹣6,0),
x2+bx+c经过原点,与x轴的另一个交点为A(﹣6,0),
∴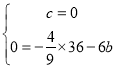 ,
,
解得: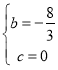 ,
,
∴抛物线解析式为:y=﹣![]() ,
,
∴顶点C(﹣3,4),
∴⊙C半径为4,
∵AO=OH=6,AD=BD,
∴OD=![]() PH,
PH,
∴PH最大时,OD有最大值,
∴当点C在PH上时,PH有最大值,
∴PH最大值为=3+![]() =3+
=3+![]() ,
,
∴OD的最大值为:![]() ,
,
故选B.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目