题目内容
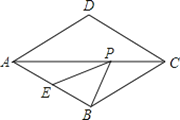
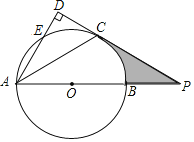
【题目】如图,AB是半圆的直径,O为圆心,点C是弧BE的中点,过点C作PC⊥AE于点D,交AB的延长线于点P
(1)求证:直线PC是⊙O的切线;
(2)若∠P=30°,AD=3,求阴影部分的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接OC,如图,由弧BC=弧CE得到∠BAC=∠EAC,加上∠OCA=∠OAC.则∠OCA=∠EAC,所以OC∥AE,从而得到PC⊥OC,然后根据切线的判定定理得到结论;
(2)解直角三角形求得AP,根据平行线分线段成比例定理求得OC,OP,利用勾股定理求得CP,然后根据S阴=S△OCP﹣S扇形BOC求解即可.
(1)连接OC.
∵点C为弧BE的中点,
∴弧BC=弧CE,
∴∠BAC=∠EAC.
∵OA=OC,
∴∠OCA=∠OAC,
∴∠OCA=∠EAC,
∴OC∥AE.
∵PC⊥AE,
∴OC⊥PC,
∴PC是⊙O的切线.
(2)在Rt△ADP中,∠P=30°,AD=3,
∴AP=2AD=6.
∵OC∥AD,
∴![]() ,
,
设OC=x,则OP=6﹣x,
∴![]() ,
,
解得:x=2,
∴OC=2,OP=4,
∴在Rt△OCP中,CP![]() 2
2![]() ,
,
∴S阴=S△OCP﹣S扇形BOC![]() OCPC
OCPC![]() 2
2![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目