题目内容
【题目】已知抛物线
:
的项点为
，交
轴于
、
两点(点在点左侧)，且
．
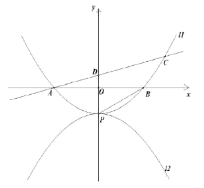
(1)求抛物线的函数解析式；
(2)过点的直线交抛物线于点
,交
轴于点
,若
的面积被轴分为1: 4两个部分，求直线
的解析式；
(3)在(2)的情况下，将抛物线绕点逆时针旋转180°得到抛物线
,点
为抛物线上一点，当点的横坐标为何值时，
为直角三角形？
【答案】（1）
；（2）直线
的解析式为
；（3）点
横坐标为
或
或
或
时，
为
．
【解析】
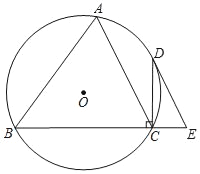
（1）求抛物线l1的顶点P（0，-2）得OP=2，由
求得BP的长，进而求得OB即点B坐标，代入抛物线l1的解析式即求得a的值．
（2）求点A坐标为（-4，0），设直线AC解析式为y=kx+b，把点A代入得b=4k，所以能用k表示点D坐标，进而用k表示△AOD和△BOD的面积．把直线AC解析式与抛物线l1解析式联立方程，即y相等时得到一个关于x的一元二次方程，解即为点A、C横坐标，利用根与系数的关系求出点C横坐标（用k表示），进而可用k表示C的纵坐标，再得到用k表示的△ABC面积．当k＞0时，显然S△AOD：S四边形OBCD=1：4，即S△AOD=
S△ABC，故得到关于k的方程，求解即得k的值．当k＜0，则得到的方程与k＞0时相同，求得的k不满足题意．综合即求得直线AC的解析式．
（3）由于不确定点B、D、M哪个为直角顶点，故需分三种情况讨论．设点M横坐标为m，①若∠BDM=90°，过M作MN⊥y轴于点N，可证△BDO∽△DMN，用m表示MN、DN的长，代入相似三角形对应边成比例即列得方程求m的值．②若∠DBM=90°，过点M作MQ⊥x轴于点Q，可证△BMQ∽△DBO，用m表示BQ、MQ的长，代入相似三角形对应边成比例即列得方程求m的值．③若∠BMD=90°，则点M在以BD为直径的圆除点B、D外的圆周上，但显然以AB为直径的圆与抛物线l2无交点，故此情况不存在满足的m．
（1）当
时，
∴顶点
，
∵
，
∴
∴
∴
∴
，代入抛物线
得：
，解得
，
∴抛物线的函数解析式为
（2）∵知抛物线交
轴于
、
两点
∴、关于
轴对称，即
∴
设直线解析式：
点代入得：
∴
∴直线：
，
∴
∵
，整理得：
∴
∵
∴
，
∴
∴
①若
，则
∴
∴
解得：
（舍去），
∴直线的解析式为
②若
，则
，
∴
解得：（舍去），（舍去）
综上所述，直线的解析式为.
（3）由（2）得：
，
∵抛物线绕点
逆时针旋转
得到抛物线
∴抛物线解析式为：
设点坐标为
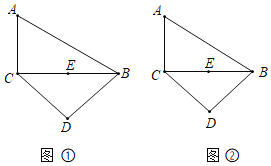
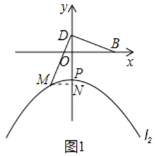
①若
，如图1，则
过作
轴于点
∴
，
，
∴
∴
∴
∴
，即
∴
解得：
，
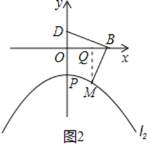
②若
，如图2，过点作
轴于点
∴
，
，
∴
∴
∴
∴
，即
∴
解得：
，
③若
，则点在以
为直径的圆除点、
外的圆周上
显然以
为真径的圆与抛物线无交点，故此情况不存在满足的
综上所述，点横坐标为或或或
时，为.
