ЬтФПФкШн
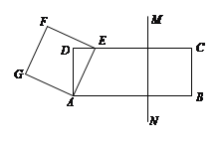
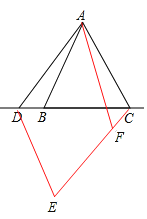
ЁОЬтФПЁПвбжЊЁїABCЮЊЕШБпШ§НЧаЮЃЌЕуDЮЊжБЯпBCЩЯЕФвЛЖЏЕуЃЈЕуDВЛгыBЁЂCжиКЯЃЉЃЌвдADЮЊБпзїСтаЮADEFЃЈAЁЂDЁЂEЁЂFАДФцЪБеыХХСаЃЉЃЌЪЙЁЯDAF=60ЁуЃЌСЌНгCFЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуDдкБпBCЩЯЪБЃЌЧѓжЄЃКЂйBD=CFЃЛЂкAC=CF+CDЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуDдкБпBCЕФбгГЄЯпЩЯЧвЦфЫћЬѕМўВЛБфЪБЃЌНсТлAC=CF+CDЪЧЗёГЩСЂЃПШєВЛГЩСЂЃЌЧыаДГіACЁЂCFЁЂCDжЎМфДцдкЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕБЕуDдкБпBCЕФбгГЄЯпЩЯЧвЦфЫћЬѕМўВЛБфЪБЃЌВЙШЋЭМаЮЃЌВЂжБНгаДГіACЁЂCFЁЂCDжЎМфДцдкЕФЪ§СПЙиЯЕ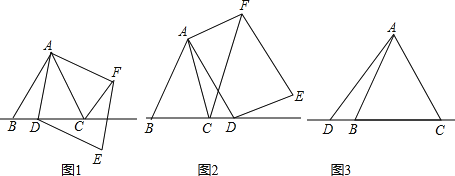
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛ
ЃЈ2ЃЉМћНтЮіЃЛ
ЃЈ3ЃЉМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊЕУГіAF=ADЃЌAB=BC=ACЃЌЁЯBAC=ЁЯDAF=60ЁуЃЌЧѓГіЁЯBAD=CAFЃЌгЩSASжЄЁїBADЁеЁїCAFЃЌЭЦГіCF=BDМДПЩЃЎ
ЃЈ2ЃЉЧѓГіЁЯBAD=ЁЯCAFЃЌИљОнSASжЄЁїBADЁеЁїCAFЃЌЭЦГіBD=CFМДПЩЃЎ
ЃЈ3ЃЉЛГіЭМаЮКѓЃЌИљОнSASжЄЁїBADЁеЁїCAFЃЌЭЦГіCF=BDМДПЩЃК
НтЃКЃЈ1ЃЉжЄУїЃКЁпЫФБпаЮAFEDЪЧСтаЮЃЌЁрAF=ADЃЎ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌЁрAB=AC=BCЃЌЁЯBAC=60Ёу=ЁЯDAFЃЎ
ЁрЁЯBACЃЁЯDAC=ЁЯDAFЃЁЯDACЃЌМДЁЯBAD=ЁЯCAFЃЎ
ЁпдкЁїBADКЭЁїCAFжаЃЌ AB=ACЃЌЁЯBAD=ЁЯCAFЃЌAD="AF" ЃЌ
ЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЎЁрCF=BDЃЎ
ЁрCF+CD=BD+CD=BC=ACЃЎ
МДЂйBD=CFЃЌЂкAC=CF+CDЃЎ
ЃЈ2ЃЉAC=CF+CDВЛГЩСЂЃЌACЁЂCFЁЂCDжЎМфДцдкЕФЪ§СПЙиЯЕЪЧAC=CFЃCDЃЎРэгЩШчЯТЃК
гЩЃЈ1ЃЉжЊЃКAB=AC=BCЃЌAD=AFЃЌЁЯBAC=ЁЯDAF=60ЁуЃЌ
ЁрЁЯBAC+ЁЯDAC=ЁЯDAF+ЁЯDACЃЌМДЁЯBAD=ЁЯCAFЃЎ
ЁпдкЁїBADКЭЁїCAFжаЃЌAC=ABЃЌЁЯBAD=ЁЯCAF ЃЌAD=AFЃЌ
ЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЎЁрBD=CFЃЎ
ЁрCFЃCD=BDЃCD=BC=ACЃЌМДAC=CFЃCDЃЎ
ВЙШЋЭМаЮШчЯТЃЌACЁЂCFЁЂCDжЎМфЕФЪ§СПЙиЯЕЮЊAC=CDЃCFЃЎ
ЃЈ3ЃЉЁпЁЯBAC=ЁЯDAF=60ЁуЃЌЁрЁЯDAB=ЁЯCAFЃЌ
ЁпдкЁїBADКЭЁїCAFжаЃЌ AB=ACЃЌЁЯDAB=ЁЯCAFЃЌ AD=AFЃЌ
ЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЎЁрCF=BDЃЎЁрCDЃCF=CDЃBD=BC=ACЃЎ

 ОйвЛЗДШ§ЦкФЉАйЗжГхДЬОэЯЕСаД№АИ
ОйвЛЗДШ§ЦкФЉАйЗжГхДЬОэЯЕСаД№АИЁОЬтФПЁПОнЁЖББОЉЭэБЈЁЗНщЩмЃЌзд2009ФъЙЪЙЌВЉЮядКФъЖШНгД§ЙлжкЪзДЮЭЛЦЦ1000ЭђШЫДЮжЎКѓЃЌУПФъНгД§СПГжајдіГЄЃЌЕН2018ФъЭЛЦЦ1700ЭђШЫДЮЃЌГЩЮЊЪРНчЩЯНгД§СПзюЖрЕФВЉЮяЙнЃЎЬиБ№ЪЧЫцзХЁЖЮвдкЙЪЙЌаоЮФЮяЁЗЁЂЁЖЩЯаТСЫЃЌЙЪЙЌЁЗЕШвЛХњЕчЪгЮФВЉНкФПЕФВЅГіЃЌЩчЛсЩЯдйДЮЯЦЦ№ЙЪЙЌШШЃЎгкЪЧЙЪЙЌЮФДДгЊЯњШЫдБЮЊПЊЗЂеыЖдВЛЭЌФъСфШКЬхЕФЮФДДВњЦЗЃЌЫцЛњЕїВщСЫВПЗжВЮЙлЙЪЙЌЕФЙлжкЕФФъСфЃЌећРэВЂЛцжЦСЫШчЯТЭГМЦЭМБэЃЎ
2018ФъВЮЙлЙЪЙЌЙлжкФъСфЦЕЪ§ЗжВМБэ
ФъСфx/Ыъ | ЦЕЪ§/ШЫЪ§ | ЦЕТЪ |
20ЁмxЃМ30 | 80 | b |
30ЁмxЃМ40 | a | 0.240 |
40ЁмxЃМ50 | 35 | 0.175 |
50ЁмxЃМ60 | 37 | c |
КЯМЦ | 200 | 1.000 |
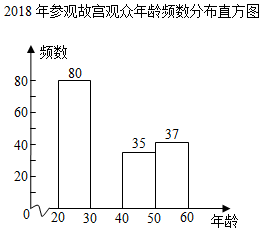
ЃЈ1ЃЉЧѓБэжаaЃЌbЃЌcЕФжЕЃЛ
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉДгЪ§ОнЩЯПДЃЌФъЧсЙлжкЃЈ20ЁмxЃМ40ЃЉвбОГЩЮЊВЮЙлЙЪЙЌЕФжївЊШКЬхЃЎШчЙћНёФъВЮЙлЙЪЙЌШЫЪ§ДяЕН2000ЭђШЫДЮЃЌФЧУДЦфжаФъЧсЙлжкдЄМЦдМга ЭђШЫДЮЃЎ