题目内容
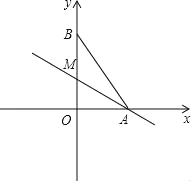
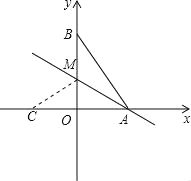
【题目】如图,在平面直角坐标系中,O为坐标原点,直角△AOB的OA边在x轴上,OB边在y轴上,且OA=6,OB=8.沿直线AM将△ABM折叠,点B正好落在x轴上,则直线AM的解析式为_____.
【答案】y=﹣![]() x+3
x+3
【解析】
设沿直线AM将△ABM折叠,点B正好落在x轴上的C点,则有AB=AC,而AB的长度根据已知可以求出,所以C点的坐标由此求出;又由于折叠得到CM=BM,在直角△CMO中根据勾股定理可以求出OM,也就求出M的坐标,而A的坐标已知,由此即可求出直线AM的解析式.
如图所示,设沿直线AM将△ABM折叠,点B正好落在x轴上的C点,
则有AB=AC,
又OA=6,OB=8,
∴AB=10,
故求得点C的坐标为:(﹣4,0).
再设M点坐标为(0,b),
则CM=BM=8﹣b,
∵CM2=CO2+OM2,
∴b=3,
∴M(0,3),而A(6,0),
∴直线AM的解析式为:y=﹣![]() x+3,
x+3,
故答案为:y=﹣![]() x+3.
x+3.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
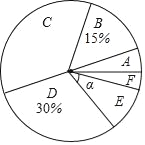
芒果教辅暑假天地重庆出版社系列答案【题目】在星期一的第八节课,我校体育老师随机抽取了九年级的总分学生进行体育中考的模拟测试,并对成绩进行统计分析,绘制了频数分布表和统计图,按得分划分成A、B、C、D、E、F六个等级,并绘制成如下两幅不完整的统计图表.
等级 | 得分x(分) | 频数(人) |
A | 95<x≤100 | 4 |
B | 90<x≤95 | m |
C | 85<x≤90 | n |
D | 80<x≤85 | 24 |
E | 75<x≤80 | 8 |
F | 70<x≤75 | 4 |
请你根据图表中的信息完成下列问题:
1)本次抽样调查的样本容量是 .其中m= ,n= .
2)扇形统计图中,求E等级对应扇形的圆心角α的度数;
3)我校九年级共有700名学生,估计体育测试成绩在A、B两个等级的人数共有多少人?
4)我校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中,随机选择2名成为学校代表参加全市体能竞赛,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
【题目】某校初级中学初一、初二、初三三个年段均有学生500人,为了解数学史知识的普及情况,按年段以2%的比例随机抽样,然后进行模拟测试,测试成绩整理如下:
初一年段 | 36 | 55 | 67 | 68 | 75 | 81 | 81 | 85 | 92 | 96 |
初二年段 | 45 | 66 | 72 | 77 | 80 | 84 | 86 | 92 | 95 | 96 |
初三年段 | 55 | 68 | 75 | 84 | 85 | 87 | 93 | 94 | 96 | 97 |
(1)估计该校学生数学史掌握水平能达到80分以上(含80分)的人数;
(2)现从样本成绩在95分以上(含95分)的学生中,任取3名参加数学史学习的经验汇报,求各年段恰好都有一名学生参加的概率.