题目内容
【题目】某校初级中学初一、初二、初三三个年段均有学生500人,为了解数学史知识的普及情况,按年段以2%的比例随机抽样,然后进行模拟测试,测试成绩整理如下:
初一年段 | 36 | 55 | 67 | 68 | 75 | 81 | 81 | 85 | 92 | 96 |
初二年段 | 45 | 66 | 72 | 77 | 80 | 84 | 86 | 92 | 95 | 96 |
初三年段 | 55 | 68 | 75 | 84 | 85 | 87 | 93 | 94 | 96 | 97 |
(1)估计该校学生数学史掌握水平能达到80分以上(含80分)的人数;
(2)现从样本成绩在95分以上(含95分)的学生中,任取3名参加数学史学习的经验汇报,求各年段恰好都有一名学生参加的概率.
【答案】(1)估计该校学生数学史掌握水平能达到80分以上(含80分)的人数为900人;(2)各年段恰好都有一名学生参加的概率=![]() .
.
【解析】
(1)用500分别乘以样本中各年级80分以上(含80分)的人数的百分比,然后求三个数的和可估计该校学生数学史掌握水平能达到80分以上(含80分)的人数;
(2)初一一个人记住A、初二两个人记作B、b、初三2个人记作C、c,利用完全列举法展示所有10种等可能的结果数,找出各年段恰好都有一名学生参加的结果数,然后根据概率公式求解.
解:(1)500×![]() +500×
+500×![]() +500×
+500×![]() =900(人),
=900(人),
所以估计该校学生数学史掌握水平能达到80分以上(含80分)的人数为900人;
(2)初一一个人记住A、初二两个人记作B、b、初三2个人记作C、c,
共有10种等可能的结果数,它们是:ABb、ABC、ABc、AbC、Abc、ACc、BbC、Bbc、BCc、bCc,
各年段恰好都有一名学生参加的结果数为4,
所以各年段恰好都有一名学生参加的概率=![]() .
.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案【题目】电器专营店的经营利润受地理位置、顾客消费能力等因素的影响,某品牌电脑专营店设有甲、乙两家分店,均销售A、B、C、D四种款式的电脑,每种款式电脑的利润如表1所示.现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式,统计各种款式电脑的销售数量,如表2所示.
表1:四种款式电脑的利润
电脑款式 | A | B | C | D |
利润(元/台) | 160 | 200 | 240 | 320 |
表2:甲、乙两店电脑销售情况
电脑款式 | A | B | C | D |
甲店销售数量(台) | 20 | 15 | 10 | 5 |
乙店销售数量(台)8 | 8 | 10 | 14 | 18 |
试运用统计与概率知识,解决下列问题:
(1)从甲店每月售出的电脑中随机抽取一台,其利润不少于240元的概率为 ;
(2)经市场调查发现,甲、乙两店每月电脑的总销量相当.现由于资金限制,需对其中一家分店作出暂停营业的决定,若从每台电脑的平均利润的角度考虑,你认为应对哪家分店作出暂停营业的决定?并说明理由.
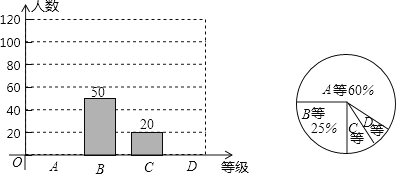
【题目】某校九年级教师在某班随机抽查了学生报考志愿的情况,绘制了如下扇形图和统计表,学生统计表绘制好后不小心撕掉了一个角.
报考学校 | 一中 | 二中 | 八中 | 其他 |
报考人数 | 4 | 5 | 6 |
(1)求撕掉角上的数和抽查学生的总数;
(2)老师打算从抽查的学生中随机抽取1个人来谈感想,求抽到报考一中学生的概率;
(3)把抽查学生的人数看做一组数据,抽查学生报考志愿人数的众数是 ,报考志愿的人数中位数是 .
(4)报考一中的人数百分比在扇形统计图中所占圆心角的正切值为 ,报考八中的百分比所占扇形统计图的圆心角的度数是 .(注:tan36°≈0.7265;tan72°≈3.078;)