题目内容
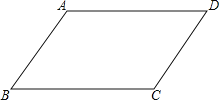
【题目】如图,在平行四边形ABCD中,
(1)以BD为对角线,作菱形MBND,使得M、N分别在BA、DC的延长线上.(保留作图痕迹,不写作图过程)
(2)证明所作四边形MBND是菱形.
【答案】(1)如图,四边形MBND为所作;见解析;(2)见解析.
【解析】
(1)连接BA、AC,它们相交于点O,再过点O作MN⊥BD分别交BA和DC的延长线于M、N,则四边形MBND为所作;
(2)由作图得到MN垂直平分BD,再证明△AOM≌△CON得到OM=ON,所以MN和BD互相垂直平分,然后可判断四边形MBND是菱形.
(1)如图,四边形MBND为所作;
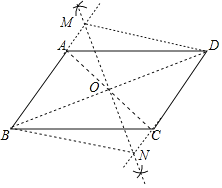
(2)利用作图得MN垂直平分BD,
∵四边形ABCD为平行四边形,
∴OA=OC,AB∥CD,
∴∠MAO=∠NCO,
而∠AOM=∠CON,
∴△AOM≌△CON(ASA),
∴OM=ON,
∴MN和BD互相垂直平分,
∴四边形MBND是菱形.

练习册系列答案
相关题目