��Ŀ����
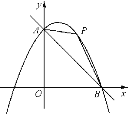
����Ŀ����ͼ1����ij����·����A��B��C������վ��һ��������Aվ���ٶ�v1����ʻ��Bվ������Bվ��ͣ���������ٶ�v2����ʻ��Cվ��������ʻ·��y(ǧ��)����ʻʱ��x(Сʱ)֮��ĺ���ͼ����ͼ2��ʾ��
(1)��������A��B��վ֮��������ʻʱ����y��x֮��ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
(2)����������ʻ·��Ϊ360ǧ��ʱ�����ʱ����ʻʱ��x��ֵ��
(3)��������ijһ��·������ʻ��90ǧ����ʱ50���ӣ�����ʻ�����·��ʱx��ֵ��

���𰸡���1��y��100x(0��x��3)����2��3.5����3��3![]()
��������
��1�������������ϵʽ������ͼ�����������ϵʽ���ٽ�y=300���룬���ɵó��𰸣�
��2�������ô���ϵ���������B��C�ĺ�����ϵʽ������y=360�����ɵó��𰸣�
��3����������0��x��3���ʱ�������ʻ��ʱ��ΪaСʱ���ٸ��������ͼ���г���a�ķ��̣����ȷ����ʻʱ�伴�ɵó��𰸣�
�⣺��1���赱������A��B��վ֮��������ʻʱ��y��x֮��ĺ�����ϵʽ��y��kx
��x=1ʱ��y=100=k��1,���k��100��
��y��100x��
��y��300ʱ��300��100x�����x��3��
�൱������A��B��վ֮��������ʻʱ��y��x֮��ĺ�����ϵʽ��y��100x(0��x��3)��
��2���赱3��x��4ʱ��y��x�ĺ�����ϵʽΪy��ax��b��
![]() ���
���![]()
�൱3��x��4ʱ��y��x�ĺ�����ϵʽΪy��120x��60��
��y��360ʱ��360��120x��60�����x��3.5��
�𣺵���������ʻ·��Ϊ360ǧ��ʱ����ʱ����ʻʱ��x��ֵ��3.5��
��3���ߵ�0��x��3ʱ��50����������ʻ��·��Ϊ(100��1)��![]() ��
��![]() ��
��![]() ��90��
��90��
��x��3ʱ��50����������ʻ��·��Ϊ[120��(4��3)]��![]() ��100��90��
��100��90��
����0��x��3���ʱ�������ʻ��ʱ��ΪaСʱ������3��x��4����ʻ��ʱ��Ϊ(![]() ��a)Сʱ��
��a)Сʱ��
(100��1)a��[120��(4��3)]��(![]() ��a)��90��
��a)��90��
���a��0.5��
��x��(3��0��5)��![]() ��
��![]() ��
��
��������ijһ��·������ʻ��90ǧ����ʱ50���ӣ���ʻ�����·��ʱx��ֵ��3![]() ��
��

 ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д� һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д� �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д�