��Ŀ����
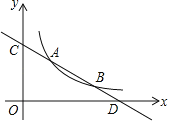
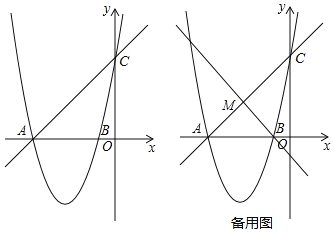
����Ŀ����ͼ��1����������y��ax2+6x+c��x����A��B���㣬��y���ڵ�C��ֱ��y��x+5������A��C��
��1���������ߵĽ���ʽ��
��2����ͼ��2����������B��ֱ�߽�ֱ��AC�ڵ�M��
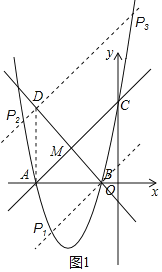
����BM��ACʱ������������һ����P�������B��C�غϣ�����ֱ��BM��ƽ���߽�AC�ڵ�Q�����Ե�B��M��Q��PΪ������ı�����ƽ���ı��Σ����P�ĺ����ꣻ
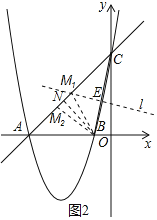
������BC����ֱ��BM��ֱ��AC�ļнǵ��ڡ�ACB��2��ʱ����ֱ��д����M�����꣮
���𰸡���1��y��x2+6x+5����2������P�ĺ�����Ϊ��4��![]() ��
��![]() ������M��������
������M��������![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��������
��1������һ�κ���ͼ���ϵ�����������������A��C�����꣬�ɵ�A��C���������ô���ϵ����������������ߵĽ���ʽ��
��2�����ö��κ���ͼ���ϵ�����������������B�����ꣻ
�����ı���BMQPΪƽ���ı��κ��ı���BMPQΪƽ���ı�������������ǣ���i�����ı���BMQPΪƽ���ı���ʱ������B��BP1��AC�����������ڵ�P1����ֱ��AC�Ľ���ʽ��ϵ�B������ɵó�ֱ��BP1�Ľ���ʽ������ֱ��BP1�������ߵĽ���ʽ�ɷ����飬ͨ���ⷽ����ɵó���P1�ĺ����ꣻ��ii�����ı���BMPQΪƽ���ı���ʱ������A��AD��y�ᣬ��ֱ��BM�ڵ�D�������D������Ϊ����5��4��������D��ֱ��P2P3��AC�����������ڵ�P2��P3����ֱ��AC�Ľ���ʽ��ϵ�D������ɵó�ֱ��P2P3�Ľ���ʽ������ֱ��P2P3�������ߵĽ���ʽ�ɷ����飬ͨ���ⷽ����������P2��P3�ĺ����ꣻ
����BC�Ĵ�ֱƽ����l������ΪE����AC�ڵ�M1����BN��AC�ڵ�N������M1���ڵ�N�ĶԳƵ�M2��M1��M2�����������ɵ�B��C����������ֱ��BC�Ľ���ʽ����E�����꣬���ֱ��l��BC�����ֱ��l�Ľ���ʽ������ֱ��l��ֱ��AC�Ľ���ʽ�ɷ����飬ͨ���ⷽ����������M1�����ꣻ��ֱ��AC�Ľ���ʽ����B�����꼰BN��AC�����ֱ��ON�Ľ���ʽ������ֱ��ON��ֱ��AC�Ľ���ʽ�ɷ����飬ͨ���ⷽ����������N�����꣬�ٽ�ϵ�NΪ�߶�M1M2���е�������M2�����꣮
��1����x��0ʱ��y��x+5��5��
���C��������0��5����
��y��0ʱ��x+5��0��
��ã�x����5��
���A����������5��0����
��A����5��0����C��0��5������y��ax2+6x+c���ã�
![]() ����ã�
����ã�![]() ��
��
�������ߵĽ���ʽΪy��x2+6x+5��
��2����y��0ʱ��x2+6x+5��0��
��ã�x1����5��x2����1��
���B����������1��0����
����PQ��BM��
�������������ǣ���ͼ1��ʾ��
��i�����ı���BMQPΪƽ���ı���ʱ������B��BP1��AC�����������ڵ�P1��
��ֱ��AC�Ľ���ʽΪy��x+5��
����ֱ��BP1�Ľ���ʽΪy��x+b��
��B����1��0������y��x+b�����1+b��0��
��ã�b��1��
��ֱ��BP1�Ľ���ʽΪy��x+1��
����ֱ��BP1�������ߵĽ���ʽ�ɷ����飬�ã�![]() ��
��
��ã�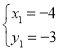 ��
��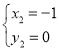 ��
��
���P1�ĺ�����Ϊ��4��
��ii�����ı���BMPQΪƽ���ı���ʱ������A��AD��y�ᣬ��ֱ��BM�ڵ�D������D��ֱ��P2P3��AC�����������ڵ�P2��P3��
��OA��OC��
���OAC��45�㣮
��BM��AC��DA��AB��
���AMB��90�㣬��ABM��45�㣬��ADM��45�㣮
�ڡ�AMD�͡�AMB�У�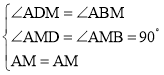 ��
��
���AMD�ա�AMB��AAS����
��AD��AB��DM��BM��
���D����������5��4����
�֡�ֱ��AC�Ľ���ʽΪy��x+5��
��ֱ��P2P3�Ľ���ʽΪy��x+9��
����ֱ��P2P3�������ߵĽ���ʽ�ɷ����飬�ã�![]() ��
��
��ã�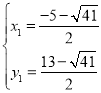 ��
��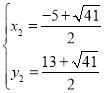 ��
��
���P2�ĺ�����Ϊ![]() ����P3�ĺ�����Ϊ
����P3�ĺ�����Ϊ![]() ��
��
������������P�ĺ�����Ϊ��4��![]() ��
��![]() ��
��
��3����BC�Ĵ�ֱƽ����l������ΪE����AC�ڵ�M1����BN��AC�ڵ�N������M1���ڵ�N�ĶԳƵ�M2��M1��M2������������ͼ2��ʾ��
�ߵ�B������Ϊ����1��0������C������Ϊ��0��5����
���E����������![]() ��
��![]() ����ֱ��BC�Ľ���ʽΪy��5x+5��
����ֱ��BC�Ľ���ʽΪy��5x+5��
��ֱ��l�Ľ���ʽΪy����![]() x+
x+![]() ��
��
����ֱ��l��ֱ��AC�Ľ���ʽ�ɷ����飬�ã�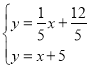 ��
��
��ã�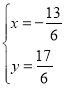 ��
��
���M1��������![]() ��
��![]() ����
����
��ֱ��AC�Ľ���ʽΪy��x+5����B������Ϊ����1��0����BN��AC��
��ֱ��ON�Ľ���ʽΪy����x��1��
����ֱ��ON��ֱ��AC�Ľ���ʽ�ɷ����飬�ã�![]() ��
��
��ã�![]() ��
��
���N����������3��2����
�֡ߵ�NΪ�߶�M1M2���е㣬
���M2��������![]() ��
��![]() ����
����
���M��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����

 ��У����ϵ�д�
��У����ϵ�д�