题目内容
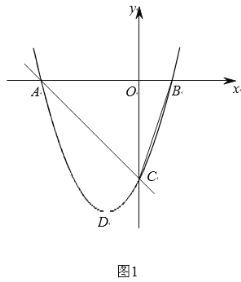
【题目】已知抛物线y=﹣x2+mx+m﹣2的顶点为A,且经过点(3,﹣3).
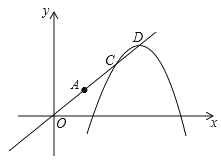
(1)求抛物线的解析式及顶点A的坐标;
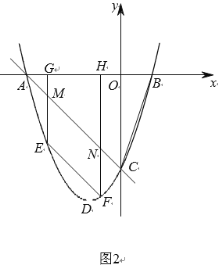
(2)将原抛物线沿射线OA方向进行平移得到新的抛物线,新抛物线与射线OA交于C,D两点,如图,请问:在抛物线平移的过程中,线段CD的长度是否为定值?若是,请求出这个定值;若不是,请说明理由.
【答案】(1)y=﹣x2+2x,顶点A的坐标是(1,1);(2)CD长为定值![]() .
.
【解析】
(1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)根据平移规律,可设出新抛物线解析式,联立抛物线与直线OA,可得C、D点的横坐标,根据勾股定理,可得答案.
解:(1)把(3,﹣3)代入y=﹣x2+mx+m-2得:﹣3=﹣32+3m+m-2,
解得m=2,
∴y=﹣x2+2x,
∴y=﹣x2+2x=﹣(x-1)2+1,
∴顶点A的坐标是(1,1);
(2)易得直线OA的解析式为y=x,
平移后抛物线顶点在直线OA上,设平移后顶点为(a,a),
∴可设新的抛物线解析式为y=﹣(x﹣a)2+a,
联立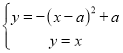
解得:x1=a,x2=a﹣1,
∴C(a-1,a-1),D(a,a),
即C、D两点间的横坐标的差为1,纵坐标的差也为1,
∴CD=![]()
∴CD长为定值![]() .
.

练习册系列答案
相关题目