题目内容
【题目】如图，已知点C是∠AOB的平分线上一点，点P、P′分别在边OA、OB上．如果要得到 OP=OP′，需要添加以下条件中的某一个即可，请你写出所有可能的结果的序号为（ ）
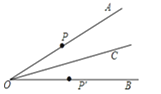
①∠OCP=∠OCP′；②∠OPC=∠OP′C；③PC=P′C；④PP′⊥OC．
A.①②B.④③C.①④③D.①②④
【答案】D
【解析】
试题因为点C是∠AOB的平分线上一点，所以∠POC=∠P′OC，当添加①∠OCP=∠OCP′后，因为OC=OC，所以由ASA可得△POC≌△P′OC，所以OP=OP′；当添加②∠OPC=∠OP′C后，因为OC=OC，所以由AAS可得△POC≌△P′OC，所以OP=OP′；当添加③PC=P′C后，因为OC=OC，不能判断△POC≌△P′OC，所以不一定得到OP=OP′；当添加④PP′⊥OC．后，设垂足为M，则∠PMC=∠P′MC=90°，又因为OM=OM，所以由ASA可得△POM≌△P′OM，所以OP=OP′；所以①②④正确，故选D．
【题目】某小区将生活垃圾分为可回收、厨余和其它三类，分别记为a，b，c，并设置了相应的垃圾箱，“可回收物”箱、“厨余垃圾”箱和“其他垃圾”箱，分别记为A，B，C.
（1）某天，小明把垃圾分装在三个袋中，可他在投放时粗心，每袋垃圾都放错了位置（每个箱中只投放一袋），请你用画树状图或列表法求小明把每袋垃圾都放错的概率；
（2）为调查居民生活垃圾分类投放情况，现随机抽取了该小区三类垃圾箱中总1000吨生活垃圾，数据统计如下（单位：吨）；
A | B | C | |
a | 240 | 30 | 30 |
b | 100 | 400 | 100 |
c | 20 | 20 | 60 |
试估计“可回收物”投放正确的概率.
【题目】骑自行车旅行越来越受到人们的喜爱，各种品牌的山地自行车相继投放市场，顺风车行经营的
型车去年6月份销售总额为3.2万元，今年经过改造升级后型车每辆销售价比去年增加400元，若今年6月份与去年6月份卖出的型车数量相同，则今年6月份型车销售总额将比去年6月份销售总额增加
．
，
两种型号车的进货和销售价格表：
|
| |
进货价格（元 | 1100 | 1400 |
销售价格（元 | 今年的销售价格 | 2400 |
（1）求今年6月份型车每辆销售价多少元；
（2）该车行计划7月份新进一批型车和型车共50辆，且型车的进货数量不超过型车数量的两倍，应如何进货才能使这批车获利最多？