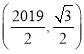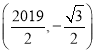题目内容
【题目】已知二次函数
（m是常数）
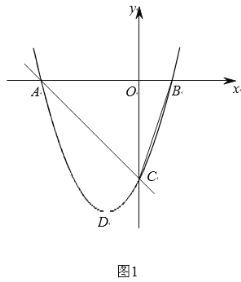
（1）证明：不论m取何值时，该二次函数图象总与x轴有两个交点；
（2）若
、
是该二次函数图象上的两个不同点，求二次函数解析式和m的值；
（3）若
，
在函数图象上，且
，求
的取值范围（结果可用含m的式子表示）.
【答案】（1）证明见详解；
（2）
，
；
（3）m-3＜x0＜m+2.
【解析】
（1）计算△的值，根据△＞0，即可解答本题；
（2）根据
、
是该二次函数图象上的两个不同点，可以求出函数的对称轴，从而可以求得m的值，得到二次函数的解析式；
（3）先计算当h=0时，x的值，然后画图象，根据图象可得结论．
解：
（1）由二次函数
可得：
，
，
则：
，
∴不论m取何值时，该二次函数图象总与x轴有两个交点；
（2）∵、是该二次函数图象上的两个不同点，
∵A，B两点y值相同，即A，B两点是对称点，
∴抛物线的对称轴是：
，
∴对称轴
，，
∴
，
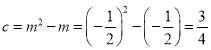
∴二次函数解析式为：；
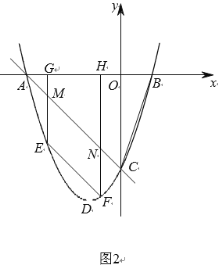
（3）当h=0时，
，
解得：
，
，
并根据抛物线的对称性，作出抛物线图像如下图所示：
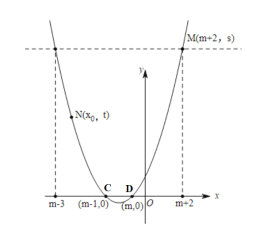
当
时，由图象得：x0的取值范围是
．
练习册系列答案
相关题目
