题目内容
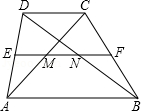
如图所示,已知梯形ABCD中,AD∥BC,且AD<BC,N、M分别为AC、BD的中点,
求证:(1)MN∥BC;(2)MN= (BC-AD).
(BC-AD).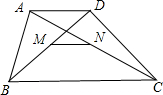
求证:(1)MN∥BC;(2)MN=
 (BC-AD).
(BC-AD).
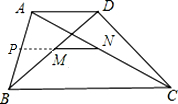
证明:(1)取AB中点P,连MP,NP,
∵M为BD的中点,
∴PM∥AD,
同理NP∥BC,
∵AD∥BC,
∴N、M、P三点共线,
∴MN∥BC.
(2)法一:∵MN∥BC,N、M分别为AC、BD的中点,
∴P是AB的中点,
∴PN= BC,PM=
BC,PM= AD,
AD,
∴MN═ (BC-AD).
(BC-AD).
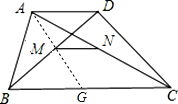
法二:如图所示,连接AM并延长,交BC于点G.
∵AD∥BC,
∴∠ADM=∠GBM,∠MAD=∠MGB,
又∵M为BD中点,
∴△AMD≌△GMB.
∴BG=AD,AM=MG.
在△AGC中,MN为中位线,
∴MN= GC=
GC= (BC-BG)=
(BC-BG)= (BC-AD),
(BC-AD),
即MN= (BC-AD).
(BC-AD).
∵M为BD的中点,
∴PM∥AD,
同理NP∥BC,
∵AD∥BC,
∴N、M、P三点共线,
∴MN∥BC.
(2)法一:∵MN∥BC,N、M分别为AC、BD的中点,
∴P是AB的中点,
∴PN=
 BC,PM=
BC,PM= AD,
AD,∴MN═
 (BC-AD).
(BC-AD).

法二:如图所示,连接AM并延长,交BC于点G.
∵AD∥BC,
∴∠ADM=∠GBM,∠MAD=∠MGB,
又∵M为BD中点,
∴△AMD≌△GMB.
∴BG=AD,AM=MG.
在△AGC中,MN为中位线,
∴MN=
 GC=
GC= (BC-BG)=
(BC-BG)= (BC-AD),
(BC-AD),即MN=
 (BC-AD).
(BC-AD).(1)取AB中点P,连MP,NP,证N、M、P三点共线即可;
(2)连接AM并延长,交BC于点G,证明△AMD≌△GMB,根据中位线定理即可证明。
(2)连接AM并延长,交BC于点G,证明△AMD≌△GMB,根据中位线定理即可证明。

练习册系列答案
相关题目
 的值。
的值。 
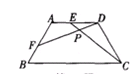
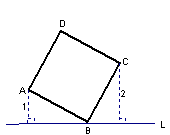
 中,
中, ,
, ,
,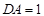 ,且
,且 ,
,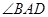 的度数;(2)四边形
的度数;(2)四边形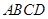 的面积(结果保留根号);
的面积(结果保留根号);
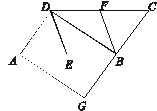
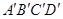 沿EF折叠,使点
沿EF折叠,使点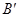 落在
落在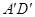 边上的点B处;沿BG折叠,使点
边上的点B处;沿BG折叠,使点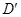 落在点D处,且BD过F点.
落在点D处,且BD过F点.