题目内容
如图，在□ABCD中，E、F分别为边AB、CD的中点，BD是对角线，过A点作AG∥BD交CB的延长线于点G．
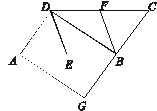
（1）求证：DE∥BF；
（2）若∠G=90°，求证：四边形DEBF是菱形．
（1）求证：DE∥BF；
（2）若∠G=90°，求证：四边形DEBF是菱形．
解：(1)在□ABCD中，AB∥CD，AB=CD
∵E、F分别为边AB、CD的中点
∴DF=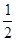
DC，BE=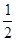AB
∴DF∥BE，DF=BE
∴四边形DEBF为平行四边形
∴DE∥BF
(2)证明： ∵AG∥BD
∴∠G=∠DBC=90°
∴△DBC为直角三角形
又∵F为边CD的中点
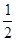∴BF=CD=DF
又∵四边形DEBF为平行四边形
∴四边形DEBF是菱形
∵E、F分别为边AB、CD的中点
∴DF=
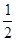DC，BE=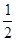AB∴DF∥BE，DF=BE
∴四边形DEBF为平行四边形
∴DE∥BF
(2)证明： ∵AG∥BD
∴∠G=∠DBC=90°
∴△DBC为直角三角形
又∵F为边CD的中点
∴BF=
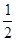CD=DF 又∵四边形DEBF为平行四边形
∴四边形DEBF是菱形
（1）根据已知条件证明BE=DF，BE∥DF，从而得出四边形DFBE是平行四边形，即可证明DE∥BF；（2）先证明DF=BF，再根据邻边相等的平行四边形是菱形，从而得出结论．
练习册系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
（BC-AD）．
ABCD中，AD=5cm，AB=3cm。AE平分∠BAD交BC于点E，则CE的长等于 （ ）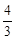
，④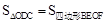
中，正确的有【 】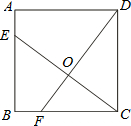
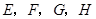分别为正方形
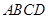的边
，
，
，
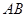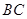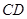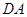上的点，且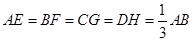
，则图中阴影部分的面积与正方形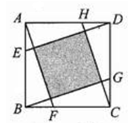
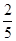
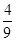
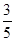
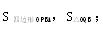
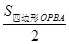< S△OQB，若存在，求出t的取值范围，若不存在，试说明理由。 