题目内容
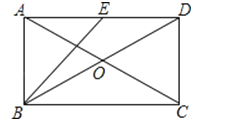
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=![]() ,则BO= ,∠EBD的大小约为 度 分.(参考数据:tan26°34′≈
,则BO= ,∠EBD的大小约为 度 分.(参考数据:tan26°34′≈![]() )
)
【答案】5;18;26
【解析】解:∵在矩形ABCD中,AC=10,
∴BD=AC=10,
∴BO=![]() BD=5,
BD=5,
∵DC=2![]() ,
,
∴AD=![]() =4
=4![]() ,
,
∴tan∠DAC=![]() =
=![]() ,
,
∵tan26°34′≈![]() ,
,
∴∠DAC≈26°34′,
∴∠OAB=∠OBA=90°﹣∠DAC=63°26′,
∵E是AD的中点,
∴AE=AB=2![]() ,
,
∴∠ABE=∠AEB=45°,
∴∠EBD=∠OBA﹣∠ABE=18°26′.
所以答案是:5,18,26.
由在矩形ABCD中,AC=10,DC=2![]() ,根据矩形的对角线相等且互相平分,可求得BO的长,利用勾股定理即可求得AD的长,继而求得∠DAC的度数,又由E是边AD的中点,可得△ABE是等腰直角三角形,继而求得答案.
,根据矩形的对角线相等且互相平分,可求得BO的长,利用勾股定理即可求得AD的长,继而求得∠DAC的度数,又由E是边AD的中点,可得△ABE是等腰直角三角形,继而求得答案.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目