题目内容
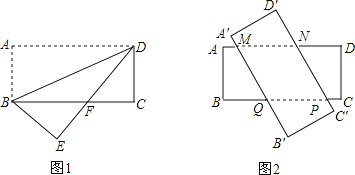
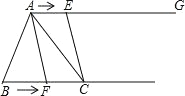
【题目】如图,在△ABC 中,BC=6cm.射线 AG∥BC,点 E 从点 A 出发沿射线 AG 以 2cm/s 的速度运动,当点 E 先出发 1s 后,点 F 也从点 B 出发沿射线 BC 以![]() cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
(1)当 t 为何值时,∠BAF<∠BAC;
(2)当 t 为何值时,AE=CF;
(3)当 t 为何值时,S△ABF+S△ACE<S△ABC.
【答案】(1) 0<t<![]() ;(2) t=
;(2) t= ![]() ,t=
,t= ![]() 时,AE=CF;(3) 当 0<t<
时,AE=CF;(3) 当 0<t<![]() 时,S△ABF+S△ACE<S△ABC.
时,S△ABF+S△ACE<S△ABC.
【解析】(1)根据边越长,边所对的角越大,可得答案;
(2)分类讨论:当点F在点C左侧时,点F再点C的右侧时,可得关于t的一元一次方程,根据解方程,可得答案;
(3)根据平行线间的距离相等,可得三角形的高相等,根据等高的三角形的底边越长,三角形的面积越大,可得不等式.
(1)当 BF<BC 时,∠BAF<∠BAC,
∴![]() t<6, 解得 t<
t<6, 解得 t<![]() ,
,
当 0<t<![]() 时,∠BAF<∠BAC;
时,∠BAF<∠BAC;
(2)分两种情况讨论:
①点 F 在点 C 左侧时,AE=CF,
则 2(t+1)=6﹣![]() t, 解得 t=
t, 解得 t=![]() ;
;
②当点F在点 C 的右侧时,AE=CF,
则 2(t+1)=![]() t, 解得 t=
t, 解得 t=![]() ,
,
综上所述,t=![]() ,t=
,t=![]() 时,AE=CF;
时,AE=CF;
(3)当 BF+AE<BC,S△ABF+S△ACE<S△ABC,![]() t+2(t+1)<6,解得 t<
t+2(t+1)<6,解得 t<![]() ,
,
当 0<t<![]() 时,S△ABF+S△ACE<S△ABC.
时,S△ABF+S△ACE<S△ABC.

【题目】小明在学习了数据的收集、整理与描述后,为妈妈整理记录了10月份的家庭支出情况,并绘制成如下尚不完整的统计图表,请你根据图表信息完成下列各题:
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | 400 |
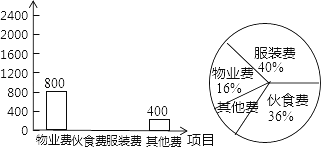
(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | ________ | ________ | 400 |
(4)请将条形统计图补充完整.