题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=2,在同一平面内,以AC为一边作等边△ACD,连接BD,则BD= ______.
【答案】2或![]()
【解析】分析:根据题意,可分为在AC的下面和在AC的上面作等边三角形,两种情况,然后根据30°角的直角三角形和等边三角形的性质以及勾股定理求解即可.
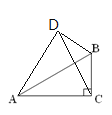
详解:根据题意,可分为D点在AC的下面:
∵∠BAC=30°,∠DAC=60°,
∴∠BAD=90°
∵∠BCA=90°
∴AB=2BC=4
根据勾股定理可得AC=AD=2![]()
∴在直角△ABD中,BD=![]() =2
=2![]() .
.
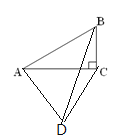
点D在AC的上面,
∵∠DAC=60°,∠BAC=30°,△ACD是等边三角形,
∴AB垂直平分CD,
∴BD=BC=2.
故答案为:2或![]() .
.

练习册系列答案
相关题目