题目内容
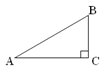
【题目】如图,△ABC内接于⊙O,弦AD⊥BC垂足为H,∠ABC=2∠CAD.
(1)如图1,求证:AB=BC;
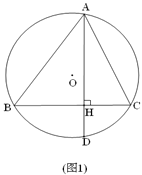
(2)如图2,过点B作BM⊥CD垂足为M,BM交⊙O于E,连接AE、HM,求证:AE∥HM;
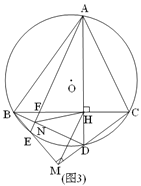
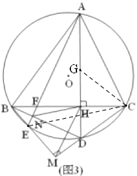
(3)如图3,在(2)的条件下,连接BD交AE于N,AE与BC交于点F,若NH=2![]() ,AD=11,求线段AB的长.
,AD=11,求线段AB的长.

【答案】(1)证明见解析;(2)证明见解析;(3)AB的长为10.
【解析】分析:(1)根据题意,设∠CAD=a,然后根据直角三角形的两锐角互余的关系,推导出∠BAC=∠ACB,再根据等角对等边得证结论;
(2)延长AD、BM交于点N,连接ED.根据圆周角定理得出∠N=∠DEN=∠BAN,进而根据等角对等边,得到DE=DN,BA=BN,再根据等腰三角形和直角三角形的性质,求得MH∥AE;
(3)连接CE,根据(2)的结论,由三角形全等的判定与性质证得HF=HC,然后结合勾股定理求出AC2-AH2=CD2-DH2,解得CD=5,CH=4,AH=8,最后根据锐角三角函数的性质得到AB.
详解:(1)证明:设∠CAD=a,
则∠ABC=2a,∠C=90°-a,∠BAD=90°-2a,
∴∠BAC=90°-2a+a=90°-a
∴∠BAC=∠ACB.∴AB=BC
(2)证明:延长AD、BM交于点N,连接ED.
∵∠DEN=∠DAB,∠N=∠BCD,∠BCD=∠BAN
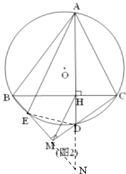
∴∠N=∠DEN=∠BAN
∴DE=DN,BA=BN
又∵BH⊥AN,DM⊥EN
∴EM=NM,HN=HA,∴MH∥AE
(3)连接CE.
∠BDA=∠BCA,∠BDM=∠BAC,由(1)知∠BCA=∠BAC
∴∠BDA=∠BDM,∴△BDM≌△BDH,
∴DH=MH,∠MBD=∠HBD,∴BD⊥MH
又∵MH∥AE,∴BD⊥EF,∴△FNB≌△ENB,
同理可证△AFH≌△ACH,∴HF=HC,又∵FN=NE
∴NH∥EC,EC=2NH,又∵NH=![]() ,∴EC=
,∴EC=![]()
∠EAC=2∠AEC=2a=∠ABC,可证弧AC=弧EC,
∴AC=EC=![]()
设HD=x,AH=11-x,
∵∠ADC=2∠CAD,翻折△CHD至△CHG,可证CG=CD=AG
AH=CD+DH,CD=AH-DH=11-x-x=11-2x
又∵AC2-AH2=CD2-DH2,∴(![]() )2-(11-x)2=(11-2x)2-x2
)2-(11-x)2=(11-2x)2-x2
∴x1=3,x2=![]() (舍去)∴CD=5,CH=4,AH=8.
(舍去)∴CD=5,CH=4,AH=8.
又∵![]() ,∴BH=6 ∴AB=
,∴BH=6 ∴AB=![]()

 学业测评一课一测系列答案
学业测评一课一测系列答案