Question

【题目】如图，正方形OABC的边OA，OC在坐标轴上，点B的坐标为（-4，4）．点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴的正方向运动，规定点P到达点O时，点Q也停止运动．连接BP，过P点作BP的垂线，与过点Q平行于y轴的直线l相交于点D．BD与y轴交于点E，连接PE．设点P运动的时间为t（s）．

（1）写出∠PBD的度数和点D的坐标（点D的坐标用t表示）；

（2）探索△POE周长是否随时间t的变化而变化，若变化，说明理由；若不变，试求这个定值．

（3）当t为何值时，△PBE为等腰三角形？

Answer 1

【答案】（1）45°，（t，t）．（2）△POE周长是定值，该定值为8．（3）当t为4秒或（4-4）秒时，△PBE为等腰三角形．

【解析】

试题（1）易证△BAP≌△PQD，从而得到DQ=AP=t，从而可以求出∠PBD的度数和点D的坐标；

（2）由于∠EBP=45°，故图1是以正方形为背景的一个基本图形，容易得到EP=AP+CE．容易得到△POE周长等于AO+CO=8，从而解决问题；

（3）EP=AP+CE，由于△PBE底边不定，故分三种情况讨论，借助于三角形全等及勾股定理进行求解，然后结合条件进行取舍，最终确定符合要求的t值．

试题解析：（1）如图1，

由题可得：AP=OQ=1×t=t（秒）

∴AO=PQ．

∵四边形OABC是正方形，

∴AO=AB=BC=OC，

∠BAO=∠AOC=∠OCB=∠ABC=90°．

∵DP⊥BP，

∴∠BPD=90°．

∴∠BPA=90°-∠DPQ=∠PDQ．

∵AO=PQ，AO=AB，

∴AB=PQ．

在△BAP和△PQD中，

∴△BAP≌△PQD（AAS）．

∴AP=QD，BP=PD．

∵∠BPD=90°，BP=PD，

∴∠PBD=∠PDB=45°．

∵AP=t，

∴DQ=t．

∴点D坐标为（t，t）．

（2）∵∠EBP=45°

∴由图1可以得到EP=CE+AP，

∴OP+PE+OE=OP+AP+CE+OE

=AO+CO

=4+4

=8．

∴△POE周长是定值，该定值为8．

（3）①若PB=PE，

由△PAB≌△DQP得PB=PD，

显然PB≠PE，

∴这种情况应舍去．

②若EB=EP，

则∠PBE=∠BPE=45°．

∴∠BEP=90°．

∴∠PEO=90°-∠BEC=∠EBC．

在△POE和△ECB中，

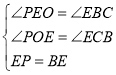
∴△POE≌△ECB（AAS）．

∴OE=CB=OC．

∴点E与点C重合（EC=0）．

∴点P与点O重合（PO=0）．

∵点B（-4，4），

∴AO=CO=4．

此时t=AP=AO=4．

③若BP=BE，

在Rt△BAP和Rt△BCE中，

∴Rt△BAP≌Rt△BCE（HL）．

∴AP=CE．

∵AP=t，

∴CE=t．

∴PO=EO=4-t．

∵∠POE=90°，

∴PE=．

延长OA到点F，使得AF=CE，连接BF，如图2所示．

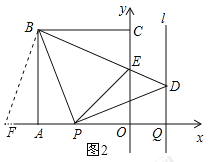
在△FAB和△ECB中，

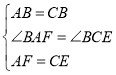
∴△FAB≌△ECB．

∴FB=EB，∠FBA=∠EBC．

∵∠EBP=45°，∠ABC=90°，

∴∠ABP+∠EBC=45°．

∴∠FBP=∠FBA+∠ABP

=∠EBC+∠ABP=45°．

∴∠FBP=∠EBP．

在△FBP和△EBP中，

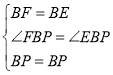
∴△FBP≌△EBP（SAS）．

∴FP=EP．

∴EP=FP=FA+AP

=CE+AP．

∴EP=t+t=2t．

∴（4-t）=2t．

解得：t=4-4

∴当t为4秒或（4-4）秒时，△PBE为等腰三角形．