Question

【题目】在圆中，、是圆的半径，点在劣弧弧上，，，∥，联结.

（1）如图1，求证：平分；

（2）点在弦的延长线上，联结，如果△是直角三角形，请你在如图2中画出

点的位置并求的长；

（3）如图3，点在弦上，与点不重合，联结与弦交于点，设点与点的

距离为，△的面积为，求与的函数关系式，并写出自变量的取值范围.

Answer 1

【答案】（1）见解析；（2）的长为或；（3），自变量的取值范围为

【解析】分析：（1）根据，得到,根据∥，得到，根据等量代换得到，即可证明.

(2) △是直角三角形只有以下两种情况:和 ，分两种情况进行讨论即可.

（3）过点作,垂足为点，根据,得到,代入即可求出与的函数关系式.

详解：（1）证明：∵、是圆的半径，

∴，

∴ ，

∵∥，

∴，

∴，

∴平分.

(2)解：由题意可知不是直角，

所以△是直角三角形只有以下两种情况:

和 ,

当，点的位置如图

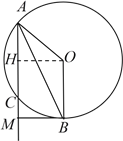
过点作,垂足为点,

∵经过圆心，∴,

∵，∴,

在Rt△中，,

∵，∴,

∵∥，∴,

∵ ，∴,

∴四边形是矩形,

∴,

∴ ,

，点的位置如图

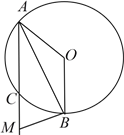
由①可知，,

在Rt△中，,

∴,

,

综上所述，的长为或.

说明：只要画出一种情况点的位置就给1分，两个点都画正确也给1分.

（3）过点作,垂足为点,

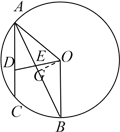
由（1）、（2）可知，,

由（2）可得： ,

∵∴ ,

∵∥，∴,

又,,,

∴ ∴ ,

∴ ,

∴ ,

自变量的取值范围为.