题目内容
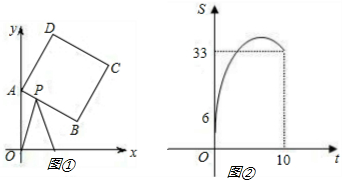
如图①,正方形ABCD中,点A、B的坐标分别为(0,12),(8,6),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q从点(1,0)出发,以相同速度沿x轴正方向运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.(1)正方形边长
(2)当P点在边AB上运动时,△OPQ的面积S与运动时间t(秒)的函数图象是如图②所示的抛物线的一部分,求点P,Q运动速度;
(3)求在(2)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;
(4)如果点P、Q保持原速度速度不变,当点P沿A?B?C?D匀速运动时,OP与PQ能否相等,若能,直接写出所有符合条件的t的值.
分析:(1)如图,在直角三角形BFA中,根据A、B的坐标可知:AF=6,BF=8,因此AB=10,即正方形的边长为10.易证△ABF≌△BCG,因此CG=BF=8,AF=BG=6,因此CH=14,FG=14,即C点的坐标为(14,14);
(2)根据图象可知:当P在AB上运动时,总共用去的时间为10s,而AB=10,因此P的速度为1,Q与P的速度相同,因此Q的速度也是1;
(3)在三角形OPQ中,OQ=1+t,关键是求出OQ边上的高,可过P作PM⊥y轴于M,根据相似三角形APM和ABF可求出AM=
t,因此OM=12-
t,根据三角形的面积公式即可求出S,t的函数关系式.根据函数的性质即可求出S的最大值及对应的t的值;
(4)本题要分四种情况进行讨论:
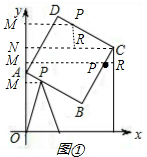 ①P在AB上,②P在BC上,③P在BC上,④P在AD上.
①P在AB上,②P在BC上,③P在BC上,④P在AD上.
选两种情况进行说明:
①P在AB上,如图:在直角三角形APM中,根据∠APM的余弦值易得出PM=
,如果OP=OQ,那么PM=
OQ,即
t=
,解得t=1.
③P在CD上,如图:在直角三角形PCR中,易知:CR=
CP=
(t-20),因此PM=RN=14-
(t-20)=30-
t,根据①的解题思路可知:PM=
OQ,即30-
t=
,解得t=
.
其它两种情况求解方法同①③.
(2)根据图象可知:当P在AB上运动时,总共用去的时间为10s,而AB=10,因此P的速度为1,Q与P的速度相同,因此Q的速度也是1;
(3)在三角形OPQ中,OQ=1+t,关键是求出OQ边上的高,可过P作PM⊥y轴于M,根据相似三角形APM和ABF可求出AM=
| 3 |
| 5 |
| 3 |
| 5 |
(4)本题要分四种情况进行讨论:
 ①P在AB上,②P在BC上,③P在BC上,④P在AD上.
①P在AB上,②P在BC上,③P在BC上,④P在AD上.选两种情况进行说明:
①P在AB上,如图:在直角三角形APM中,根据∠APM的余弦值易得出PM=
| 3t |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| 1+t |
| 2 |
③P在CD上,如图:在直角三角形PCR中,易知:CR=
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| 1+t |
| 2 |
| 295 |
| 13 |
其它两种情况求解方法同①③.
解答: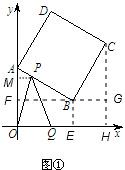 解:(1)10,(14,14);
解:(1)10,(14,14);
(2)由图象知,点P在AB上运动时间10,路程是10,所以点P,Q速度为1;
(3)作BE⊥x轴于E,BF⊥y轴于F,过P作PM⊥y轴于M,
由△APM∽△ABF易得OM=12-
t,
S=
(1+t)(12-
t)=-
t2+
t+6,
所以t=9.5时S有最大值.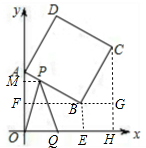
此时点P(7.6,6.3);
(4)t=1,t=
.
 解:(1)10,(14,14);
解:(1)10,(14,14);(2)由图象知,点P在AB上运动时间10,路程是10,所以点P,Q速度为1;
(3)作BE⊥x轴于E,BF⊥y轴于F,过P作PM⊥y轴于M,
由△APM∽△ABF易得OM=12-
| 3 |
| 5 |
S=
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| 57 |
| 10 |
所以t=9.5时S有最大值.

此时点P(7.6,6.3);
(4)t=1,t=
| 295 |
| 13 |
点评:本题主要考查了正方形的性质、坐标与图形性质、三角形相似、图形面积的求法、等腰三角形的性质以及二次函数的应用等知识点.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上) (2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
(2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
 如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )
如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )