题目内容
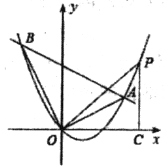
【题目】如图,在平面直角坐标系中抛物线![]() 经过原点,且与直线
经过原点,且与直线![]() 交于则
交于则![]() 、
、![]() 两点.
两点.
(1)求直线和抛物线的解析式;
(2)点![]() 在抛物线上,解决下列问题:
在抛物线上,解决下列问题:
①在直线![]() 下方的抛物线上求点
下方的抛物线上求点![]() ,使得
,使得![]() 的面积等于20;
的面积等于20;
②连接![]() ,作
,作![]() 轴于点
轴于点![]() ,若
,若![]() 和
和![]() 相似,请直接写出点
相似,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() 的坐标为
的坐标为![]() 或
或![]() ;②点
;②点![]() 的坐标为:
的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)把![]() 代入
代入![]() 即可求出一次函数解析式,把
即可求出一次函数解析式,把![]() 、
、![]() 代入
代入![]() 即可求出二次函数解析式;
即可求出二次函数解析式;
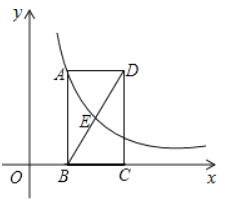
(2)①如图1,作![]() 轴,交
轴,交![]() 于点
于点![]() ,设
,设![]() ,则
,则![]() ,表示出PQ、AB的长,然后根据三角形的面积公式列式求解即可;
,表示出PQ、AB的长,然后根据三角形的面积公式列式求解即可;
②先根据勾股定理及其逆定理求出![]() ,然后分当
,然后分当![]() 时和当
时和当![]() 时两种情况求解即可.
时两种情况求解即可.
(1)把![]() 代入
代入![]() ,得
,得
![]() ,
,
![]() ,
,
![]() 直线解析式为
直线解析式为![]() ,
,
∵抛物线![]() 经过原点,
经过原点,
∴c=0.
把![]() 、
、![]() 代入
代入![]() ,得
,得
由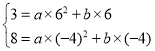 ,
,
得抛物线解析式为![]() ;
;
(2)①如图1,作![]() 轴,交
轴,交![]() 于点
于点![]() ,
,
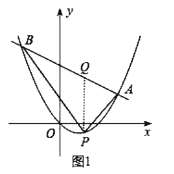
设![]() ,则
,则![]() ,
,
![]() ,AB=6+4=10,
,AB=6+4=10,
![]() ,
,
解得![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
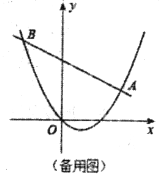
②设![]() ,如图2,
,如图2,
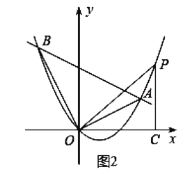
由题意得:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
即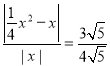 ,
,
整理得![]() ,
,
解方程![]() ,得
,得![]() (舍去),
(舍去),![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;
;
解方程![]() 得
得![]() (舍去),
(舍去),![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;
;
当![]() 时,
时,![]() ,即
,即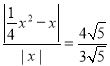 ,
,
整理得![]() ,
,
解方程![]() ,得
,得![]() (舍去),
(舍去),![]() ,此时
,此时![]() 点坐标
点坐标![]() ;
;
解方程![]() ,得
,得![]() (舍去),
(舍去),![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;
;
综上所述:点![]() 的坐标为:
的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目