题目内容
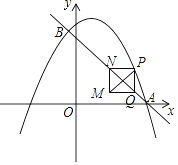
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
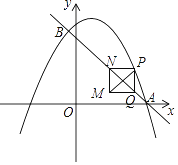
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
【答案】(1)![]() ,
, ![]() ;(2)m<﹣
;(2)m<﹣![]() 或0<m<3;(3)C=﹣2(m﹣
或0<m<3;(3)C=﹣2(m﹣![]() )2+
)2+![]() ,﹣
,﹣![]() <m<
<m<![]() 且m≠0;(4)m<﹣
且m≠0;(4)m<﹣![]() .
.
【解析】试题分析:(1)先确定出点A,B的坐标,最后用待定系数法即可得出结论。
(2)点P在抛物线上,点Q在直线y=﹣x+3上,点N在直线AB上,设出点P的坐标,再表示出Q、N的坐标,即可得出PN=PQ,再用MN与y轴在PQ的同侧,建立不等式即可得出结论。
(3)点P在点A,B之间的抛物线上,根据(2)可知PQ的长,设正方形PQMN的周长为C,根据C=4PQ,建立C与m的函数关系式,求出其顶点坐标,根据二次函数的性质,即可求得结论。
(4)分两种情况讨论计算即可求出结论。
(1)解:∵直线y=﹣x+3与x轴相交于点A,
∴A(3,0),
∵点B在直线y=﹣x+3上,且B的横坐标为﹣ ![]() ,
,
∴B(﹣ ![]() ,
, ![]() ),
),
∵A,B在抛物线上,
∴ 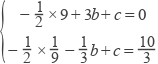 ,
,
∴ ![]()
(2)解:方法1、由(1)知,b= ![]() ,c=
,c= ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,
,
设P(m,﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ),
),
∵点Q在直线y=﹣x+3上,
∴Q(m,﹣m+3),
∵点N在直线AB上,
∴N(( ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() ),(﹣
),(﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() )),
)),
∴PN=| ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() ﹣m|=|
﹣m|=| ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() |
|
∴PQ=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ﹣(﹣m+3)|=|﹣
﹣(﹣m+3)|=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() |,
|,
∵四边形PQMN时正方形,
∴PN=PQ,
∴| ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() |=|﹣
|=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() |,此时等式恒成立,
|,此时等式恒成立,
当m<0且m≠﹣ ![]() 时,
时,
∵MN与y轴在PQ的同侧,
∴点N在点P右侧,
∴ ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() >m,
>m,
∴m<﹣ ![]() ,
,
当m>0且m≠3时,
∵MN与y轴在PQ的同侧,
∴点P在点N的右侧,
∴ ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() <m,
<m,
∴﹣ ![]() <m<3,
<m<3,
∴0<m<3,
即:m的范围为m<﹣ ![]() 或0<m<3;
或0<m<3;
方法2、如图,

记直线AB与y轴的交点为D,
∵直线AB的解析式为y=﹣x+3,
∴D(0,3),
∴OD=3,
∵A(3,0),
∴OA=3,
∴OA=OB,
∴∠ODA=45°,
∵PQ∥y轴,
∴∠PQB=45°,
记:直线PN交直线AB于N',
∵四边形PQMN是正方形,
∴∠QPN=90°,
∴∠PN'Q=45°=∠PQN',
∴PQ=PN',
∵四边形PQMN是正方形,
∴PQ=PN,
点N在点P的左侧时,点N'都在直线AB上,
∵MN与y轴在PQ的同侧,
∴m的范围为m<﹣ ![]() 或0<m<3
或0<m<3
(3)解:由(1)知,b= ![]() ,c=
,c= ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,
,
设P(m,﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ),
),
∵点Q在直线y=﹣x+3上,
∴Q(m,﹣m+3),
∴PQ=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ﹣(﹣m+3)|=|﹣
﹣(﹣m+3)|=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() |,
|,
∵点P在点A,B之间的抛物线上,
∴PQ=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ,(﹣
,(﹣ ![]() <m<3且m≠0),
<m<3且m≠0),
∵设正方形PQMN的周长为C,
∴C=4PQ=4(﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() )=﹣2m2+
)=﹣2m2+ ![]() m+2=﹣2(m﹣
m+2=﹣2(m﹣ ![]() )2+
)2+ ![]() ,
,
∵C随m增大而增大,
∴m< ![]() ,
,
∴﹣ ![]() <m<
<m< ![]() 且m≠0
且m≠0
(4)解:当△PQM与坐标轴有2个公共点时,
∴m<0或0<m<3
当0<m<3,PN>yP ,
由(2)知,P(m,﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ),PQ=|﹣
),PQ=|﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() |=﹣
|=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]()
∵四边形PQMN是正方形,
∴PN=PQ=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() >﹣
>﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ,
,
∴m>3,所以,此种情况不符合题意;
当m<0时,PN>yP ,
∵PQ= ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() ,
,
∵四边形PQMN是正方形,
∴PN=PQ= ![]() m2﹣
m2﹣ ![]() m﹣
m﹣ ![]() >﹣
>﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ,
,
∴m>3(舍)或m<﹣ ![]() ,
,
即:当△PQM与坐标轴有2个公共点时,m<﹣ ![]() .
.