��Ŀ����
��֪����ͼ�����κ���y=a��x+1��2-4��ͼ����x��ֱ���A��B���㣬��y�ύ�ڵ�D����C�Ƕ��κ���y=a��x+1��2-4��ͼ��Ķ��㣬CD=
��
��1����a��ֵ��
��2����M�ڶ��κ���y=a��x+1��2-4ͼ��ĶԳ����ϣ��ҡ�AMC=��BDO�����M�����꣮
��3�������κ���y=a��x+1��2-4��ͼ������ƽ��k��k��0������λ��ƽ�ƺ��ͼ����ֱ��CD�ֱ���E��F���㣨��F�ڵ�E��ࣩ����ƽ�ƺ�Ķ��κ�����ͼ��Ķ���ΪC1����y��Ľ���ΪD1���Ƿ����ʵ��k��ʹ��CF��FC1�������ڣ����k��ֵ���������ڣ���˵�����ɣ�

| 2 |
��1����a��ֵ��
��2����M�ڶ��κ���y=a��x+1��2-4ͼ��ĶԳ����ϣ��ҡ�AMC=��BDO�����M�����꣮
��3�������κ���y=a��x+1��2-4��ͼ������ƽ��k��k��0������λ��ƽ�ƺ��ͼ����ֱ��CD�ֱ���E��F���㣨��F�ڵ�E��ࣩ����ƽ�ƺ�Ķ��κ�����ͼ��Ķ���ΪC1����y��Ľ���ΪD1���Ƿ����ʵ��k��ʹ��CF��FC1�������ڣ����k��ֵ���������ڣ���˵�����ɣ�

��1����C��-1��-4����CD=
��
��D��0��-3��
��a=1
��y=��x+1��2-4
��y=x2+2x-3��
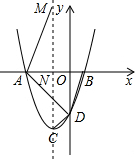 ��2������ͼ���������߶Գ�����x��Ľ���ΪN����N��-1��0����
��2������ͼ���������߶Գ�����x��Ľ���ΪN����N��-1��0����
�ɣ�1���������ߣ�y=x2+2x-3���ã�A��-3��0����B��1��0��
��Rt��OBD��OD=3��OB=1��tan��BDO=
=
��
����AMC=��BDO����tan��AMN=tan��BDO=
��
��Rt��AMN��AN=OA-ON=2��MN=AN��tan��AMN=6��
��M��-1��6����-1��-6����
 ��3�����ڣ�
��3�����ڣ�
��CC1=DD1=k��CC1��DD1��
���ı���CC1D1DΪƽ���ı��Σ�
��C1D1��CD��
���D1C1C=��DCN=45�㣬
��CF��FC1��
���CC1F=45��
����CFC1Ϊ����ֱ�������Σ���CC1=k��
��F��-
k-1��-
k-4����
�ɵ�F����������y=x2+2x-3-k�ϣ�
�ࣨ-
k-1��2+2��-
k-1��-3-k=-
k-4��
���k=2��k=0���ᣩ��
��k=2��
��k=2ʱ��CF��FC1��
| 2 |
��D��0��-3��
��a=1
��y=��x+1��2-4
��y=x2+2x-3��
 ��2������ͼ���������߶Գ�����x��Ľ���ΪN����N��-1��0����
��2������ͼ���������߶Գ�����x��Ľ���ΪN����N��-1��0�����ɣ�1���������ߣ�y=x2+2x-3���ã�A��-3��0����B��1��0��
��Rt��OBD��OD=3��OB=1��tan��BDO=
| OB |
| OD |
| 1 |
| 3 |
����AMC=��BDO����tan��AMN=tan��BDO=
| 1 |
| 3 |
��Rt��AMN��AN=OA-ON=2��MN=AN��tan��AMN=6��
��M��-1��6����-1��-6����
 ��3�����ڣ�
��3�����ڣ���CC1=DD1=k��CC1��DD1��
���ı���CC1D1DΪƽ���ı��Σ�
��C1D1��CD��
���D1C1C=��DCN=45�㣬
��CF��FC1��
���CC1F=45��
����CFC1Ϊ����ֱ�������Σ���CC1=k��
��F��-
| 1 |
| 2 |
| 1 |
| 2 |
�ɵ�F����������y=x2+2x-3-k�ϣ�
�ࣨ-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
���k=2��k=0���ᣩ��
��k=2��
��k=2ʱ��CF��FC1��

��ϰ��ϵ�д�
 һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д� ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
�����Ŀ
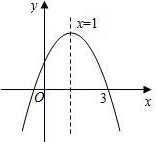
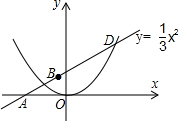
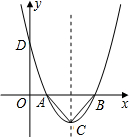
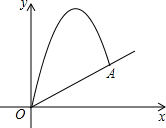

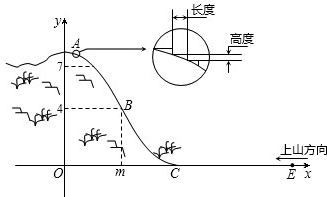 ����������������ո߶ȣ�
����������������ո߶ȣ� ______m2��______m2������Щ���У�xȡ______mʱ�����S���
______m2��______m2������Щ���У�xȡ______mʱ�����S���