题目内容
已知二次函数y=(t+1)x2+2(t+2)x+
在x=0和x=2时的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数y=kx+6的图象与二次函数的图象都经过点A(-3,m),求m和k的值;
(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移n(n>0)个单位后得到的图象记为G,同时将(2)中得到的直线y=kx+6向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,求n的取值范围.

| 3 |
| 2 |
(1)求二次函数的解析式;
(2)若一次函数y=kx+6的图象与二次函数的图象都经过点A(-3,m),求m和k的值;
(3)设二次函数的图象与x轴交于点B,C(点B在点C的左侧),将二次函数的图象在点B,C间的部分(含点B和点C)向左平移n(n>0)个单位后得到的图象记为G,同时将(2)中得到的直线y=kx+6向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,求n的取值范围.

(1)∵二次函数y=(t+1)x2+2(t+2)x+
在x=0和x=2时的函数值相等,
∴代入得:0+0+
=4(t+1)+4(t+2)+
,
解得:t=-
,
∴y=(-
+1)x2+2(-
+2)x+
=-
x2+x+
,
∴二次函数的解析式是y=-
x2+x+
.
(2)把A(-3,m)代入y=-
x2+x+
得:m=-
×(-3)2-3+
=-6,
即A(-3,-6),
代入y=kx+6得:-6=-3k+6,
解得:k=4,
即m=-6,k=4.
(3)由题意可知,点B、C间的部分图象的解析式是y=-
x2+x+
=-
(x2-2x-3)=-
(x-3)(x+1),-1≤x≤3,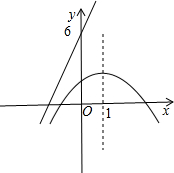
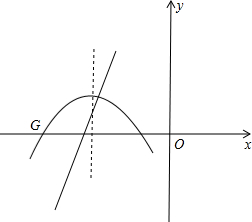
则抛物线平移后得出的图象G的解析式是y=-
(x-3+n)(x+1+n),-n-1≤x≤3-n,
此时直线平移后的解析式是y=4x+6+n,
如果平移后的直线与平移后的二次函数相切,
则方程4x+6+n=-
(x-3+n)(x+1+n)有两个相等的实数解,
即-
x2-(n+3)x-
n2-
=0有两个相等的实数解,
判别式△=[-(n+3)]2-4×(-
)×(-
n2-
)=6n=0,
即n=0,
∵与已知n>0相矛盾,
∴平移后的直线与平移后的抛物线不相切,
∴结合图象可知,如果平移后的直线与抛物线有公共点,
则两个临界的交点为(-n-1,0),(3-n,0),
则0=4(-n-1)+6+n,
n=
,
0=4(3-n)+6+n,
n=6,
即n的取值范围是:
≤n≤6.
| 3 |
| 2 |
∴代入得:0+0+
| 3 |
| 2 |
| 3 |
| 2 |
解得:t=-
| 3 |
| 2 |
∴y=(-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴二次函数的解析式是y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)把A(-3,m)代入y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
即A(-3,-6),
代入y=kx+6得:-6=-3k+6,
解得:k=4,
即m=-6,k=4.
(3)由题意可知,点B、C间的部分图象的解析式是y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


则抛物线平移后得出的图象G的解析式是y=-
| 1 |
| 2 |
此时直线平移后的解析式是y=4x+6+n,
如果平移后的直线与平移后的二次函数相切,
则方程4x+6+n=-
| 1 |
| 2 |
即-
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
判别式△=[-(n+3)]2-4×(-
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
即n=0,
∵与已知n>0相矛盾,
∴平移后的直线与平移后的抛物线不相切,
∴结合图象可知,如果平移后的直线与抛物线有公共点,
则两个临界的交点为(-n-1,0),(3-n,0),
则0=4(-n-1)+6+n,
n=
| 2 |
| 3 |
0=4(3-n)+6+n,
n=6,
即n的取值范围是:
| 2 |
| 3 |

练习册系列答案
相关题目