题目内容
【题目】一张正方形纸的内部被针扎了2010个孔，这些孔和正方形的顶点之中的任何3点都不共线．作若干条互不相交的线段，它们的端点都是这些孔或正方形的顶点，这些线段将正方形分割成一些三角形，并且在这些三角形的内部和边上都不再有小孔．请问一共作了多少条线段？共得到了多少个三角形？
【答案】一共作了6031条线段，共得到4022个三角形．
【解析】
（1）画出简单图形，从中找出规律，根据规律解答即可；
（2）根据每个三角形有3条边，每条边都是与另一个三角形的公共边解答即可.
（1）如图，
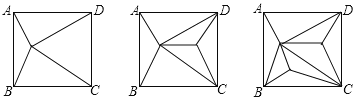
有1个点时，内部分割成4个三角形；
有2个点时，内部分割成4+2=6个三角形；
那么有3个点时，内部分割成4+2×2=8个三角形；
有4个点时，内部分割成4+2×3=10个三角形；
……
∴有n个点时，内部分割成4+2×（n-1）=（2n+2）个三角形；
∴有2010个点时，内部分割2×2010+2=4022个三角形；
（2）这4022个三角形共有4022×3条边，其中有4条边是原正方形的4条边，不用另行作出，其他各边都是作出的线段，每条线段恰为两个三角形的公共边，故作出的线段总数为（4022×3﹣4）÷2＝6031．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
