题目内容
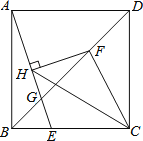
【题目】在正方形ABCD中,点E为BC边上一点且CE=2BE,点F为对角线BD上一点且BF=2DF,连接AE交BD于点G,过点F作FH⊥AE于点H,连结CH、CF,若HG=2cm,则△CHF的面积是______cm2.
【答案】![]()
【解析】
如图,过F作FI⊥BC于I,连接FE,FA,得到FI∥CD,设BE=EI=IC=a,CE=FI=2a,AB=3a,由勾股定理得到FE=FC=FA=![]() a,推出HE=
a,推出HE=![]() AE=
AE=![]() a,根据正方形的性得到BG平分∠ABC,由三角形角平分线定理得到
a,根据正方形的性得到BG平分∠ABC,由三角形角平分线定理得到![]() ,求得HG=
,求得HG=![]() AE=
AE=![]() a=2,于是得到结论.
a=2,于是得到结论.
解:如图,过F作FI⊥BC于I,连接FE,FA,
∴FI∥CD,
∵CE=2BE,BF=2DF,
∴设BE=EI=IC=a,CE=FI=2a,AB=3a,
∴则FE=FC=FA=![]() a,
a,
∴H为AE的中点,
∴HE=![]() AE=
AE=![]() a,
a,
∵四边形ABCD是正方形,
∴BG平分∠ABC,
∴![]()
∴HG=![]() AE=
AE=![]() a=2,
a=2,
∴a=![]() ,
,
∴S△CHF=S△HEF+S△CEF-S△CEH=![]() (
(![]() a)2+
a)2+![]() 2a2a-
2a2a-![]() 2a
2a![]() a=
a=![]() a2=
a2=![]() ,
,

故答案为:![]() .
.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目