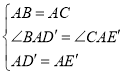题目内容
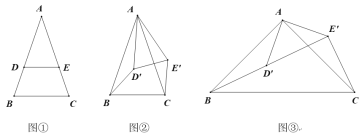
【题目】如图,点![]() 是等边三角形
是等边三角形![]() 内一点,且
内一点,且![]() ,
,![]() ,
,![]() ,若将
,若将![]() 绕着点
绕着点![]() 逆时针旋转后得到
逆时针旋转后得到![]() ,则
,则![]() 的度数是_______.
的度数是_______.

【答案】![]()
【解析】
首先证明△BDE为等边三角形,得∠BED=60°,由△ABD≌CBE可得EC=DA,在△DEC中,已知三边,用勾股定理逆定理证出得出∠DEC=90°,可求∠BEC的度数,由此即可解决问题.
根据旋转的性质知△ABD≌△CBE,
则EB=DB=4,DA=EC=3,∠ABD=∠CBE,
∵△ABC是等边三角形,
∴∠ABC=∠ABD+∠DBC=60°,
∴∠DBE=∠CBE+∠DBC=60°,
∴△BDE为等边三角形,
∴DE=DB=BE=4,
又∵DE=4,DC=5,EC=3,
∴DE2+EC2=DC2,
∴∠DEC=90°,
∵△BDE为等边三角形,
∴∠BED=60°,
∴∠BEC=∠BED+∠DEC=150°,
∴∠ADB=∠BEC=150°.
故答案为:150°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目