题目内容
【题目】如图,抛物线![]() 与坐标轴交于点
与坐标轴交于点![]() ,点
,点![]() 和点
和点![]() ,连接
,连接![]() .
.
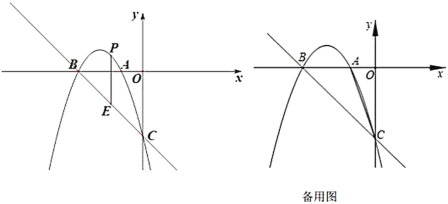
(1)求抛物线的解析式;
(2)如图,已知点![]() 在线段
在线段![]() 的上方(不包括点
的上方(不包括点![]() 和点
和点![]() ),过
),过![]() 点作
点作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,求线段
,求线段![]() 的最大值;
的最大值;
(3)该抛物线上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为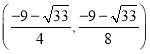 、
、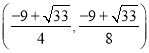 、
、![]() 或
或![]() .
.
【解析】
(1)把![]() ,点
,点![]() 和点
和点![]() 代入抛物线解析式
代入抛物线解析式![]() 组成三元一次方程组,解方程组,即可得抛物线的系数a、b、c的值,代入抛物线解析式即可.
组成三元一次方程组,解方程组,即可得抛物线的系数a、b、c的值,代入抛物线解析式即可.
(2)因为点P在抛物线上,所以设![]() ,而
,而![]() 的直线方程为
的直线方程为![]() ,所以
,所以![]() ,所以
,所以![]() ,利用二次函数性质求得PE的最大值为;
,利用二次函数性质求得PE的最大值为;
(3)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,由题意求得
,由题意求得![]() ,再根据相似三角形的性质可得
,再根据相似三角形的性质可得![]() ,
,![]() ,进而证出
,进而证出![]() 是等腰直角三角
是等腰直角三角![]()
![]() ,从而求得
,从而求得![]() ,设
,设![]() ,①当
,①当![]() 或
或![]() 时,点
时,点![]() 在点
在点![]() 左侧或在
左侧或在![]() 之间,横纵坐标均为负数,
之间,横纵坐标均为负数,![]() ,
,![]() ,所以
,所以![]() ,列方程解即可得P的坐标;②当
,列方程解即可得P的坐标;②当![]() 或
或![]() 时,点
时,点![]() 在
在![]() 之间或在点
之间或在点![]() 右侧,横纵坐标异号
右侧,横纵坐标异号![]() ,列方程即可得P点的坐标;
,列方程即可得P点的坐标;
(1)∵抛物线与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,与y轴交于点
,与y轴交于点![]()
∴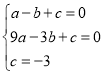
∴
∴抛物线解析式为![]()
(2)设![]() ,
,![]() 的直线方程为
的直线方程为![]()
∴![]() ,∴
,∴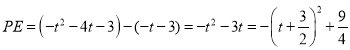
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]()
(3)如图1,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]()

∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]() 是等腰直角三角形∴
是等腰直角三角形∴![]()
∴![]()
∴![]()
∴![]()
设![]()
①当![]() 或
或![]() 时,点
时,点![]() 在点
在点![]() 左侧或在
左侧或在![]() 之间,横纵坐标均为负数
之间,横纵坐标均为负数
∴![]() ,
,![]()
∴![]()
解得:![]() ,,
,,![]()
 或
或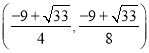
②当![]() 或
或![]() 时,点
时,点![]() 在
在![]() 之间或在点
之间或在点![]() 右侧,横纵坐标异号
右侧,横纵坐标异号
∴![]()
解得:![]() ,
,![]()
∴![]() 或
或![]()
综上所述,点![]() 的坐标为
的坐标为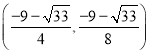 、
、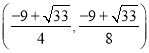 、
、![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差.根据表中数据,要从中选择一名成绩好且发挥稳定的同学参加数学竞赛,应该选择__________(填“甲”, “乙”, “丙”, “丁”).
甲 | 乙 | 丙 | 丁 | |
平均数(分) | 92 | 95 | 95 | 92 |
方差 | 3.6 | 3.6 | 7.4 | 8.1 |
【题目】某超市计划购进一批A、B两种规格的端午节礼盘进行销售,进价和售价如下表所示:
端午节礼盘规格 | A | B |
进价(元/盘) | 80 | 100 |
售价(元/盘) | 120 | 160 |
若购进两种规格的端午节礼盒共300盒,且投入资金不超过26800元.
(1)该超市应购进A规格端午节礼盒至少多少盒?
(2)若超市购进A规格端午节礼盒的进价每盒降低a元,并保持这两个规格的端午节礼盒的售价不变,且最多购进240盒A规格端午节礼盒.如果这批端午节礼盒售出后,超市刚好获利18480元,求a的取值范围.
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某学校为了了解学生对新型冠状病毒肺炎防护知识的掌握情况,随机抽取若干名同学利用网络进行了“新冠状病毒肺炎防疫知识”问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成![]() 、
、![]() 、
、![]() 、
、![]() 四组,绘制了如下统计图表:
四组,绘制了如下统计图表:
“新冠状病毒肺炎防疫知识”问卷测试成绩统计表
组别 | 分数/分 | 频数 | 各组总分/分 |
|
| 38 | 2581 |
|
|
| 5543 |
|
| 60 | 5100 |
|
| 30 | 2796 |
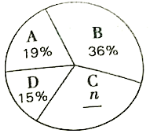
依据以上统计信息,解答下列问题:
(1)求得![]() ,
,![]() ;
;
(2)这次测试成绩的中位数落在 组;
(3)求本次全部测试成绩的平均数.