��Ŀ����
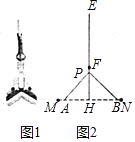
����Ŀ����ͼ�ڣ���![]() �У�AC��8cm��BC��6cm����P�ӵ�A��������б��AB���B�����˶����ٶ�Ϊ
�У�AC��8cm��BC��6cm����P�ӵ�A��������б��AB���B�����˶����ٶ�Ϊ![]() ������P��PQ��AB��AC�ڵ�Q����PQΪһ����������PQMN��ʹ��N��������PB�ϣ�����CM����CQ=y���˶�ʱ��Ϊx��s����0��x��
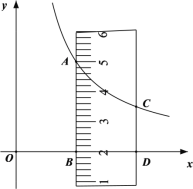
������P��PQ��AB��AC�ڵ�Q����PQΪһ����������PQMN��ʹ��N��������PB�ϣ�����CM����CQ=y���˶�ʱ��Ϊx��s����0��x��![]() ����y��x������ϵ��ͼ����ʾ��
����y��x������ϵ��ͼ����ʾ��
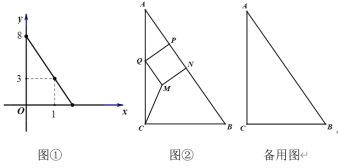
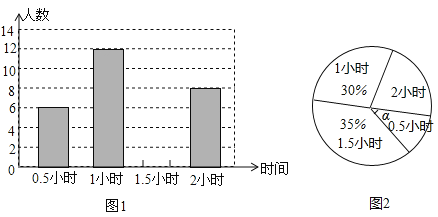
��1����y��x������ϵʽ��a��ֵ��
��2����![]() �����ΪS����S�����ֵ��
�����ΪS����S�����ֵ��
��3����![]() �ǵ��������Σ���x��ֵ��
�ǵ��������Σ���x��ֵ��
���𰸡���1��![]() ��a��ֵΪ4����2��
��a��ֵΪ4����2��![]() ����3��x��ֵΪ1��
����3��x��ֵΪ1��![]() ��
��![]() ��
��
��������
��1�����ô���ϵ�����������y��x������ϵʽ����![]() ʱ��
ʱ��![]() ���Ӷ������AQ�ij����ٸ������������ε��ж������ʿ����AP�ij����ɴ˼��ɵó�a��ֵ��
���Ӷ������AQ�ij����ٸ������������ε��ж������ʿ����AP�ij����ɴ˼��ɵó�a��ֵ��
��2����ͼ���������������������������ε����ʿ����PQ�ij����Ӷ��ɵ�MQ�ij����������������Ǻ����ɵ�DM�ij���Ȼ�����������ε������ʽ�ɵ�S��x�ĺ�����ϵʽ��������ö��κ�����������⼴�ɣ�
��3���������߶εĺͲ���ɶ������![]() ��ֵ���ٸ��ݵ��������εĶ��������������ֱ���������⼴�ɵã�
��ֵ���ٸ��ݵ��������εĶ��������������ֱ���������⼴�ɵã�
��1����y��x������ϵʽΪ![]()
��ͼ�ٿ�֪��![]() ��ͼ����
��ͼ����![]()
����![]() ����ã�
����ã�![]() �����
�����![]()
��y��x������ϵʽΪ![]()
��![]() ʱ��
ʱ��![]() ����
����![]()
![]() ��
��![]()
![]() ��
��![]()
![]() �ı���PQMN��������
�ı���PQMN��������
![]()
![]()
��![]() ��
��![]() ��
�У�![]()
![]()
![]() ����
����![]()
���![]()
��![]()
���ϣ�y��x������ϵʽΪ![]() ��a��ֵΪ4��
��a��ֵΪ4��
��2�����˶�ʱ��Ϊ![]() ʱ
ʱ
�ɣ�1����֪��![]() ��
��![]() ��
��![]()
![]() ����
����![]()
���![]()
![]() �ı���PQMN��������
�ı���PQMN��������
![]() ��
��![]()
![]()
![]()
![]()
��![]() ��
�У�![]()
��![]() ��
��![]() ����
����![]()
���![]()
��![]()
�����ã�![]()
�ɶ��κ��������ʿ�֪����![]() ʱ��Sȡ�����ֵ�����ֵΪ
ʱ��Sȡ�����ֵ�����ֵΪ![]() ��
��
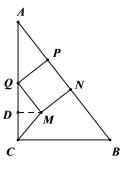
��3����![]() ��
�У�![]()
![]()
��![]() ��
�У�![]()
�ɵ��������εĶ��壬���������������
�ٵ�![]() ʱ��
ʱ��![]() �ǵ���������
�ǵ���������
��![]()
���![]()
�ڵ�![]() ʱ��
ʱ��![]() �ǵ���������
�ǵ���������
��![]() ����
����![]()
���![]() ��
��![]() ���������⣬��ȥ��
���������⣬��ȥ��
�۵�![]() ʱ��
ʱ��![]() �ǵ���������
�ǵ���������
��![]() ����
����![]()
���![]() ��
��![]() ���������⣬��ȥ��
���������⣬��ȥ��
���ϣ�x��ֵΪ1��![]() ��
��![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�