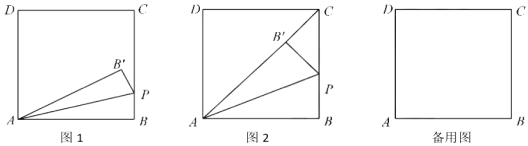
题目内容
【题目】(问题情境)
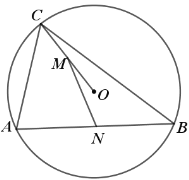
如图①,在△ABC中,AB=AC,点D、E分别为线段AB、AC上的点,且DE∥BC.将△ADE绕点A旋转一定的角度后得到△AD′E′,如图②.
(1)求证:△ABD′≌△ACE′.
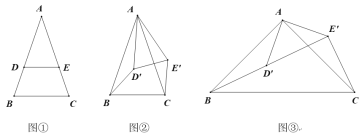
(深入研究)
如图③,![]() ,
,![]() ,
,![]() .
.
(2)若点D′在线段BE′上,求△BCE′的面积.
(3)若点B、D′、E′不在同一直线上,且点![]() 在
在![]() 内,顺次连结C、B、D′、E′四点,则四边形CBD′E′的面积是否改变,若改变,请求出改变后的面积;若不变,请说明理由.
内,顺次连结C、B、D′、E′四点,则四边形CBD′E′的面积是否改变,若改变,请求出改变后的面积;若不变,请说明理由.
(拓展延伸)
(4)如图④,在四边形ABCD中,AB∥CD,∠D=∠C≠90°.请用没有刻度的直尺和圆规画出满足下列条件的四边形A′B′CD.
条件1:利用一次旋转变换改变线段AB的位置,得到对应线段A′B′.
条件2:连结A′D、B′C,使得四边形A′B′CD的面积与四边形ABCD的面积相等.

【答案】(1)见解析;(2)6;(3)不变,理由见解析;(4)见解析
【解析】
①根据旋转后角和线段不变可证明出△ABD′≌△ACE′.
②根据全等三角形对应边,对应角相等可得出![]() 是直角三角形,根据勾股定理求出x或关于x的一个等式,从而可以求出
是直角三角形,根据勾股定理求出x或关于x的一个等式,从而可以求出![]() 的面积.
的面积.
③根据全等和面积的加减法可求出四边形CBD′E′的面积不变
④借助第三问的结论构造出两个三角形,即可画出图形.
(1)由题意得:![]()
![]()
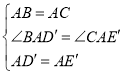
∴![]()
2)同理(1)可得![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
∴![]()
![]() ,设
,设![]()
![]() +
+![]() =
=![]()
化简得:![]()
∴![]()
(3)不变
理由如下:
∵![]() ,
,![]() ,
,![]()
∴△ABC的面积为8,△![]() 的面积为2
的面积为2
∵![]()
∴![]()
∴![]() =
=![]()
∴![]() 的大小不变
的大小不变
(4)如图,
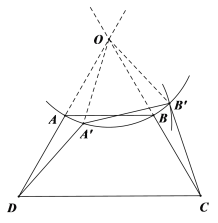
如图所示的四边形A′B′CD就是所画的四边形

【题目】下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差.根据表中数据,要从中选择一名成绩好且发挥稳定的同学参加数学竞赛,应该选择__________(填“甲”, “乙”, “丙”, “丁”).
甲 | 乙 | 丙 | 丁 | |
平均数(分) | 92 | 95 | 95 | 92 |
方差 | 3.6 | 3.6 | 7.4 | 8.1 |