��Ŀ����
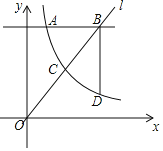
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y����![]() x2+bx+c��x�ύ��B��C���㣬��y�ύ�ڵ�A��ֱ��y����
x2+bx+c��x�ύ��B��C���㣬��y�ύ�ڵ�A��ֱ��y����![]() x+2����A��C���㣬�����ߵĶԳ�����x�ύ�ڵ�D��ֱ��MN��Գ��ύ�ڵ�G���������߽���M��N���㣨��N�ڶԳ����Ҳࣩ����MN��x�ᣬMN��7��
x+2����A��C���㣬�����ߵĶԳ�����x�ύ�ڵ�D��ֱ��MN��Գ��ύ�ڵ�G���������߽���M��N���㣨��N�ڶԳ����Ҳࣩ����MN��x�ᣬMN��7��
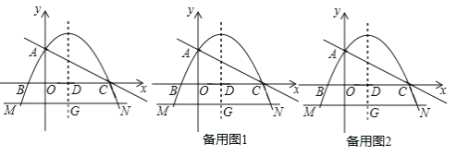
��1����������ߵĽ���ʽ��
��2�����N�����꣮
��3������A��ֱ���������߽��ڵ�F����tan��FAC��![]() ʱ�����F�����꣮
ʱ�����F�����꣮
��4������D��ֱ��AC�Ĵ��ߣ���AC�ڵ�H����y���ڵ�K������CN����AHK������AC��ÿ��1����λ���ȵ��ٶ��ƶ����ƶ������С�AHK���ı���DGNC�����ص������ص����ΪS���ƶ�ʱ��Ϊt��0��t��![]() ������ֱ��д��S��t�ĺ�����ϵʽ��
������ֱ��д��S��t�ĺ�����ϵʽ��
���𰸡���1��y����![]() x2+
x2+![]() x+2����2����N��������5��-3������3����F����������3��2����
x+2����2����N��������5��-3������3����F����������3��2����![]() ����
����![]() ������4��
������4��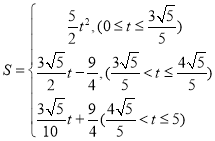 ��
��
��������
��1����A��C������ֱ�Ϊ��0��2������4��0��������A��C������������߱���ʽ������⣻
��2�������ߵĶԳ���Ϊ��x��![]() ����N�ĺ�����Ϊ��
����N�ĺ�����Ϊ��![]() ��������⣻
��������⣻
��3���ֵ�F��ֱ��AC�·�����F��ֱ��AC���Ϸ�����������ֱ���⼴�ɣ�
��4����0��t��![]() ����
����![]() ��t��
��t��![]() ��
��![]() ��t��
��t��![]() ����������ֱ���⼴�ɣ�
����������ֱ���⼴�ɣ�
�⣺��1��ֱ��y����![]() x+2����A��C���㣬���A��C������ֱ�Ϊ��0��2������4��0����
x+2����A��C���㣬���A��C������ֱ�Ϊ��0��2������4��0����
��c��2�������߱���ʽΪ��y����![]() x2+bx+2��
x2+bx+2��
����C���������ʽ����ã�b��![]() ��
��
�������ߵı���ʽΪ��y����![]() x2+
x2+![]() x+2���٣�
x+2���٣�
��2�������ߵĶԳ���Ϊ��x��![]() ��
��
��N�ĺ�����Ϊ�� ![]() ��
��
�ʵ�N������Ϊ��5��-3����
��3����tan��ACO��![]() ��tan��FAC��
��tan��FAC��![]() ��
��
����ACO����FAC��
�ٵ���F��ֱ��AC�·�ʱ��
��ֱ��AF��x���ڵ�R��

�ߡ�ACO����FAC����AR��CR��
���R��r��0������r2+4����r��4��2����ã�r��![]() ��
��
����R����������![]() ��0����
��0����
����R��A���������һ�κ�������ʽ��y��mx+n�ã� ��
��
��ã� ��
��
��ֱ��AR�ı���ʽΪ��y����![]() x+2���ڣ�
x+2���ڣ�
�����٢ڲ���ã�x��![]() ���ʵ�F��
���ʵ�F��![]() ����
����![]() ����
����
�ڵ���F��ֱ��AC���Ϸ�ʱ��
�ߡ�ACO����F��AC����AF���x�ᣬ
���F�䣨3��2����
���ϣ���F������Ϊ����3��2����![]() ����
����![]() ����
����
��4����ͼ2�����ACO��������tan����![]() ����sin����
����sin����![]() ��cos����
��cos����![]() ��
��
�ٵ�0��t��![]() ʱ�����ͼ����
ʱ�����ͼ����
���AHK�ƶ�����A��H��K���λ��ʱ��ֱ��H��K��ֱ�x���ڵ�T���������߶Գ����ڵ�S��

���DST����ACO����������T��TL��KH��
��LT��HH�䣽t����LTD����ACO������
��DT�� ��DS��
��DS��![]() ��
��
S��S��DST��![]() DT��DS��
DT��DS��![]() ��
��
�ڵ�![]() ��t��
��t��![]() ʱ���Ҳ�ͼ����
ʱ���Ҳ�ͼ����
ͬ���ɵã�
S��![]() ��
��![]() DG����GS��+DT�䣩��
DG����GS��+DT�䣩��![]() 3+��
3+��![]() +
+![]() ��
��![]() ����
����![]() ��
��
�۵�![]() ��t��
��t��![]() ʱ��ͬ���ɵ�S=
ʱ��ͬ���ɵ�S=![]() ��
��
���ϣ�S�� ��
��

 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�����Ŀ���±���¼�˼ס��ҡ�����������ͬѧ���������ѧ���Գɼ���ƽ�����뷽����ݱ������ݣ�Ҫ����ѡ��һ���ɼ����ҷ����ȶ���ͬѧ�μ���ѧ������Ӧ��ѡ��__________������������ �������� �������� ����������
�� | �� | �� | �� | |
ƽ�������֣� | 92 | 95 | 95 | 92 |
���� | 3.6 | 3.6 | 7.4 | 8.1 |