Question

【题目】已知抛物线的顶点为P，与y轴交于点A，与直线OP交于点B.

（1）如图1，若点P的横坐标为1，点， ，试确定抛物线的解析式；

（2）在（1）的条件下，若点M是直线AB下方抛物线上的一点，且S△ABM=3，求点M的坐标；

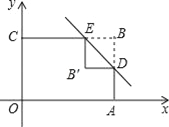
（3）如图2，若P在第一象限，且，过点P作轴于点D，将抛物线平移，平移后的抛物线经过点A、D，该抛物线与轴的另一个交点为C，请探索四边形OABC的形状，并说明理由.

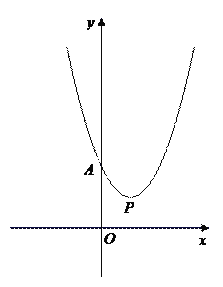
图1 图2

Answer 1

【答案】（1）；（2）(1, 2) 或 (2, 3).；（3）四边形OABC是矩形，理由见解析

【解析】（1）利用顶点P的横坐标求出b=-2,然后把b=-2和B点的坐标代入求出抛物线的解析式；

（2）先求出A点坐标，然后得出直线AB的解析式，设M点坐标为（x，x2-2x+3），根据S△ABM=3列出方程，并解方程，从而得出M点坐标；

（3）根据抛物线的图象可求出A、P、D的坐标，利用抛物线与直线相交求出B点坐标，然后求出平移后抛物线的解析式，然后求出C点坐标，然后求出BC的长度，从而得出四边形OABC是平行四边形，再根据∠AOC=90得出四边形OABC是矩形.

解：（1）依题意, , 解得b=-2.

将b=-2及点B(3, 6)的坐标代入抛物线解析式

得 . 解c=3. 所以抛物线的解析式为.

（2）∵抛物线 与y轴交于点A，

∴ A(0, 3).

∵ B(3, 6), 可得直线AB的解析式为.

设直线AB下方抛物线上的点M坐标为（x， ），过M点作y轴的平行线交直线AB于点N, 则N(x, x+3). (如图1)

图1

∴.

∴.

解得 .

∴点M的坐标为(1, 2) 或 (2, 3).

（3）如图2，由 PA=PO, OA=c, 可得.

图2

∵抛物线的顶点坐标为 ,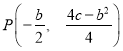

∴.

∴.

∴ 抛物线,

A（0， ），P（， ）, D（，0）.

可得直线OP的解析式为.

∵ 点B是抛物线与直线的图象的交点，

令 .

解得.

可得点B的坐标为（-b， ）.

由平移后的抛物线经过点A, 可设平移后的抛物线解析式为.

将点D(，0)的坐标代入，得.

∴ 平移后的抛物线解析式为.

令y=0, 即. 解得.

依题意, 点C的坐标为（-b，0）.

∴ BC=.

∴ BC= OA.

又BC∥OA，

∴ 四边形OABC是平行四边形.

∵ ∠AOC=90，

∴ 四边形OABC是矩形.