题目内容
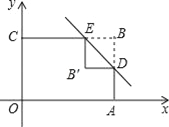
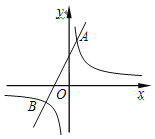
【题目】已知一次函数y1=2x+m的图象与反比例函数y2=![]() 的图象交于A,B两点,且点A的横坐标为1.
的图象交于A,B两点,且点A的横坐标为1.
(1)求一次函数的表达式;
(2)若反比例函数在第一象限的图象上有一点C到y轴的距离为3,求△ABC的面积.
【答案】(1)一次函数的表达式为y1=2x+4;
(2)S△ABC =16
【解析】试题分析:(1)把点A的横坐标,代入反比例函数解析式求出点A的纵坐标,从而得到点A的坐标,再利用待定系数法求直线解析式即可;(2)根据点C到y轴的距离判断出点C的横坐标,代入反比例函数解析式求出纵坐标,从而得到点C的坐标,过点C作CD∥x轴交直线AB于D,求出点D的坐标,然后得到CD的长度,再联立一次函数与双曲线解析式求出点B的坐标,然后△ABC的面积=△ACD的面积+△BCD的面积,列式进行计算即可得解
试题解析:
解:(1)∵点A的横坐标为1,代入反比例函数表达式,得y2=![]() =6
=6
∴点A的坐标为(1,6)
又∵点A在一次函数y1=2x+m的图象上
∴2+m=6,∴m=4
∴一次函数的表达式为y1=2x+4
(2)由题意知点C的横坐标为3,代入反比例函数表达式
得y2=![]() =2,
=2,
∴点C的坐标为(3,2)
过点C作CD∥x轴交直线AB于D,则点D的纵坐标为2
∴2x+4=2,∴x=-1,∴D(-1,2)
∴CD=4
由 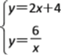 解得
解得 ![]()
![]()
∴点B的坐标为(-3,-2)
∴S△ABC =S△ACD +S△BCD = ![]() CD·( yA-yB )=
CD·( yA-yB )=![]() ×4×( 6+2 )=16
×4×( 6+2 )=16

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目